for $0 < x \leq 1 / 2$ ,
$\ln Γ (x) \approx - \ln (x) + x R_{n, m}^{1} (x + 1);$
for $1 / 2 < x \leq 3 / 2$ ,
$\ln Γ (x) \approx (x - 1) R_{n, m}^{1} (x);$
for $3 / 2 < x \leq 4$ ,
$\ln Γ (x) \approx (x - 2) R_{n, m}^{2} (x);$
for $4 < x \leq 12$ ,
$\ln Γ (x) \approx R_{n, m}^{3} (x);$
and for $12 < x$ ,
$\ln Γ (x) \approx (x - \frac{1}{2}) \ln (x) - x + \ln (\sqrt{2 π}) + \frac{1}{x} R_{n, m}^{4} (1 / x^{2}) .$ (1)

For each expansion, the specific values of

n

and

m

are selected to be minimal such that the maximum relative error in the expansion is of the order

10^{- d}

, where

d

is the maximum number of decimal digits that can be accurately represented for the particular implementation (see nag_machine_decimal_digits (x02be)).

Let

ε

denote machine precision and let

x_{huge}

denote the largest positive model number (see nag_machine_real_largest (x02al)). For

x < 0.0

the value

\ln Γ (x)

is not defined; nag_specfun_gamma_log_real (s14ab) returns zero and exits with

ifail = 1

. It also exits with

ifail = 1

when

x = 0.0

, and in this case the value

x_{huge}

is returned. For

x

in the interval

(0.0, ε]

, the function

\ln Γ (x) = - \ln (x)

to machine accuracy.

Now denote by

x_{big}

the largest allowable argument for

\ln Γ (x)

on the machine. For

{(x_{big})}^{1 / 4} < x \leq x_{big}

the

R_{n, m}^{4} (1 / x^{2})

term in Equation (1) is negligible. For

x > x_{big}

there is a danger of setting overflow, and so nag_specfun_gamma_log_real (s14ab) exits with

ifail = 2

and returns

x_{huge}

References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

Cody W J and Hillstrom K E (1967) Chebyshev approximations for the natural logarithm of the gamma function Math.Comp. 21 198–203

Parameters

Compulsory Input Parameters

1: $x$ – double scalar: The argument $x$ of the function.

Constraint: $x > 0.0$ .

Optional Input Parameters

None.

Output Parameters

1: $result$ – double scalar: The result of the function.
2: $ifail$ – int64int32nag_int scalar: $ifail = 0$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Errors or warnings detected by the function:

Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.

$ifail = 1$: On entry, $x \leq 0.0$ . If $x < 0.0$ the function is undefined; on soft failure, the function value returned is zero. If $x = 0.0$ and soft failure is selected, the function value returned is the largest machine number (see nag_machine_real_largest (x02al)).

W $ifail = 2$: On entry, $x > x_{big}$ (see Description). On soft failure, the function value returned is the largest machine number (see nag_machine_real_largest (x02al)).

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.

$ifail = - 999$: Dynamic memory allocation failed.

Accuracy

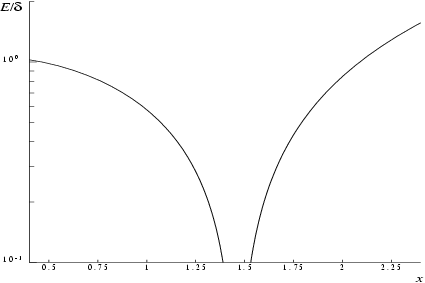
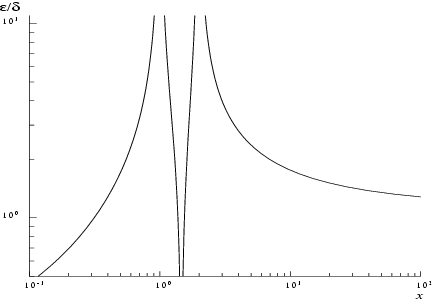
Let

δ

and

ε

be the relative errors in the argument and result respectively, and

E

be the absolute error in the result.

δ

is somewhat larger than machine precision, then

E ≃ |x \times Ψ (x)| δ and ε ≃ |\frac{x \times Ψ (x)}{\ln Γ (x)}| δ

where

Ψ (x)

is the digamma function

\frac{Γ^{'} (x)}{Γ (x)}

. Figure 1 and Figure 2 show the behaviour of these error amplification factors.

Figure 1

Figure 2

These show that relative error can be controlled, since except near

x = 1 ​ or ​ 2

relative error is attenuated by the function or at least is not greatly amplified.

For large

x

ε ≃ (1 + \frac{1}{\ln x}) δ

and for small

x

ε ≃ \frac{1}{\ln x} δ

The function

\ln Γ (x)

has zeros at

x = 1

and

2

and hence relative accuracy is not maintainable near those points. However absolute accuracy can still be provided near those zeros as is shown above.

If however,

δ

is of the order of machine precision, then rounding errors in the function's internal arithmetic may result in errors which are slightly larger than those predicted by the equalities. It should be noted that even in areas where strong attenuation of errors is predicted the relative precision is bounded by the effective machine precision.

Further Comments

None.

Example

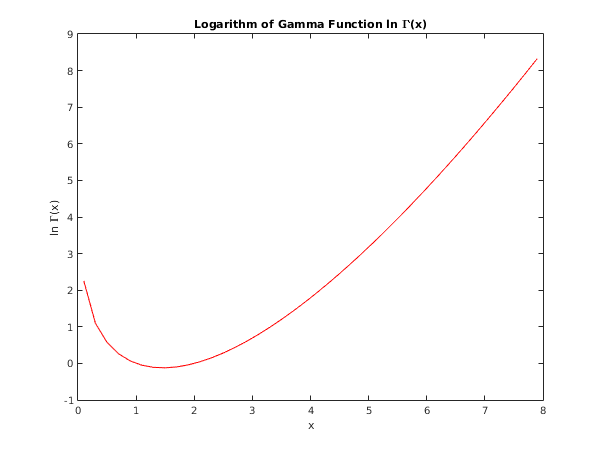
This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

Open in the MATLAB editor: s14ab_example

function s14ab_example


fprintf('s14ab example results\n\n');

x = [ 1   1.25    1.5    1.75    2     5    10    20   1000];
n = size(x,2);
result = x;

for j=1:n
  [result(j), ifail] = s14ab(x(j));
end

disp('      x       log_gamma(x)');
fprintf('%12.3e%12.3e\n',[x; result]);

s14ab_plot;



function s14ab_plot
  x = [0.1:0.2:8];

  for j=1:numel(x)
    [lg(j), ifail] = s14ab(x(j));
  end

  fig1 = figure;
  plot(x,lg,'-r');
  xlabel('x');
  ylabel('ln \Gamma(x)');
  title('Logarithm of Gamma Function ln \Gamma(x)');
  axis([0 8 -1 9]);

s14ab example results

      x       log_gamma(x)
   1.000e+00   0.000e+00
   1.250e+00  -9.827e-02
   1.500e+00  -1.208e-01
   1.750e+00  -8.440e-02
   2.000e+00   0.000e+00
   5.000e+00   3.178e+00
   1.000e+01   1.280e+01
   2.000e+01   3.934e+01
   1.000e+03   5.905e+03

PDF version (NAG web site, 64-bit version, 64-bit version)

Chapter Contents

Chapter Introduction

NAG Toolbox