1: $result$ – double scalar: The result of the function.
2: $ifail$ – int64int32nag_int scalar: $ifail = 0$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Errors or warnings detected by the function:

$ifail = 1$: The function has been called with an argument greater than or equal to $1.0$ in magnitude, for which $arctanh$ is not defined. On soft failure, the result is returned as zero.

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.

$ifail = - 999$: Dynamic memory allocation failed.

Accuracy

δ

and

ε

are the relative errors in the argument and result, respectively, then in principle

|ε| ≃ |\frac{x}{(1 - x^{2}) arctanh x} \times δ| .

That is, the relative error in the argument,

x

, is amplified by at least a factor

\frac{x}{(1 - x^{2}) arctanh x}

in the result. The equality should hold if

δ

is greater than the machine precision (

δ

due to data errors etc.) but if

δ

is simply due to round-off in the machine representation then it is possible that an extra figure may be lost in internal calculation round-off.

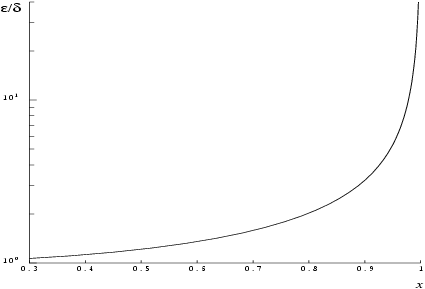
The behaviour of the amplification factor is shown in the following graph:

Figure 1

The factor is not significantly greater than one except for arguments close to

|x| = 1

. However in the region where

|x|

is close to one,

1 - |x| \sim δ

, the above analysis is inapplicable since

x

is bounded by definition,

|x| < 1

. In this region where arctanh is tending to infinity we have

ε \sim 1 / \ln δ

which implies an obvious, unavoidable serious loss of accuracy near

|x| \sim 1

, e.g., if

x

and

1

agree to

6

significant figures, the result for

arctanh x

would be correct to at most about one figure.

Further Comments

None.

Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

Open in the MATLAB editor: s11aa_example

function s11aa_example


fprintf('s11aa example results\n\n');

x = [-0.5     0    0.5     -0.9999];
n = size(x,2);
result = x;

for j=1:n
  [result(j), ifail] = s11aa(x(j));
end

disp('      x        arctanh(x)');
fprintf('%12.3e%12.3e\n',[x; result]);

s11aa example results

      x        arctanh(x)
  -5.000e-01  -5.493e-01
   0.000e+00   0.000e+00
   5.000e-01   5.493e-01
  -9.999e-01  -4.952e+00

PDF version (NAG web site, 64-bit version, 64-bit version)

Chapter Contents

Chapter Introduction

NAG Toolbox