NAG Toolbox: nag_tsa_cp_binary_user (g13ne)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{n}$ – int64int32nag_int scalar

$n$, the length of the time series.

Constraint: $\mathbf{n}\ge 2$.

2:     $\mathrm{beta}$ – double scalar

$\beta$, the penalty term.

There are a number of standard ways of setting $\beta$, including:

SIC or BIC

$\beta =p\times \log \left(n\right)$.

AIC

$\beta =2p$.

Hannan-Quinn

$\beta =2p\times \log \left(\log \left(n\right)\right)$.

where $p$ is the number of parameters being treated as estimated in each segment. The value of $p$ will depend on the cost function being used.

If no penalty is required then set $\beta =0$. Generally, the smaller the value of $\beta$ the larger the number of suggested change points.

3:     $\mathrm{chgpfn}$ – function handle or string containing name of m-file

chgpfn must calculate a proposed change point, and the associated costs, within a specified segment.

[v, cost, user, info] = chgpfn(side, u, w, minss, user, info)

Input Parameters

1:     $\mathrm{side}$ – int64int32nag_int scalar

Flag indicating what chgpfn must calculate and at which point of the Binary Segmentation it has been called.

$\mathbf{side}=-1$

only $C\left(y_{u:w}\right)$ need be calculated and returned in $\mathbf{cost}\left(1\right)$, neither v nor the other elements of cost need be set. In this case, $u=1$ and $w=\mathrm{n}$.

$\mathbf{side}=0$

all elements of cost and v must be set. In this case, $u=1$ and $w=\mathrm{n}$.

$\mathbf{side}=1$

the segment, $y_{u:w}$, is a left hand side subsegment from a previous iteration of the Binary Segmentation algorithm. All elements of cost and v must be set.

$\mathbf{side}=2$

the segment, $y_{u:w}$, is a right hand side subsegment from a previous iteration of the Binary Segmentation algorithm. All elements of cost and v must be set.

The distinction between $\mathbf{side}=1$ and $2$ may allow for chgpfn to be implemented in a more efficient manner. See section Example for one such example.

The first call to chgpfn will always have $\mathbf{side}=-1$ and the second call will always have $\mathbf{side}=0$. All subsequent calls will be made with $\mathbf{side}=1$ or $2$.

2:     $\mathrm{u}$ – int64int32nag_int scalar

$u$, the start of the segment of interest.

3:     $\mathrm{w}$ – int64int32nag_int scalar

$w$, the end of the segment of interest.

4:     $\mathrm{minss}$ – int64int32nag_int scalar

The minimum distance between two change points, as passed to nag_tsa_cp_binary_user (g13ne).

5:     $\mathrm{user}$ – Any MATLAB object

chgpfn is called from nag_tsa_cp_binary_user (g13ne) with the object supplied to nag_tsa_cp_binary_user (g13ne).

6:     $\mathrm{info}$ – int64int32nag_int scalar

$\mathbf{info}=0$.

Output Parameters

1:     $\mathrm{v}$ – int64int32nag_int scalar

If $\mathbf{side}=-1$ then v need not be set.

if $\mathbf{side}\ne -1$ then $v$, the proposed change point. That is, the value which minimizes

$$\underset{v}{\mathrm{minimize}}C\left(y_{u:v}\right)+C\left(y_{v+1:w}\right)$$

for $v=u+\mathbf{minss}-1$ to $w-\mathbf{minss}$.

2:     $\mathrm{cost}\left(3\right)$ – double array

Costs associated with the proposed change point, $v$.

If $\mathbf{side}=-1$ then $\mathbf{cost}\left(1\right)=C\left(y_{u:w}\right)$ and the remaining two elements of cost need not be set.

If $\mathbf{side}\ne -1$ then

• $\mathbf{cost}\left(1\right)=C\left(y_{u:v}\right)+C\left(y_{v+1:w}\right)$.
• $\mathbf{cost}\left(2\right)=C\left(y_{u:v}\right)$.
• $\mathbf{cost}\left(3\right)=C\left(y_{v+1:w}\right)$.

3:     $\mathrm{user}$ – Any MATLAB object

4:     $\mathrm{info}$ – int64int32nag_int scalar

In most circumstances info should remain unchanged.

If info is set to a strictly positive value then nag_tsa_cp_binary_user (g13ne) terminates with $\mathbf{ifail}=\mathbf{51}$.

If info is set to a strictly negative value the current segment is skipped (i.e., no change points are considered in this segment) and nag_tsa_cp_binary_user (g13ne) continues as normal. If info was set to a strictly negative value at any point and no other errors occur then nag_tsa_cp_binary_user (g13ne) will terminate with $\mathbf{ifail}=\mathbf{52}$.

Optional Input Parameters

1:     $\mathrm{minss}$ – int64int32nag_int scalar

Default: $2$

The minimum distance between two change points, that is ${\tau }_i-{\tau }_{i-1}\ge \mathbf{minss}$.

Constraint: $\mathbf{minss}\ge 2$.

2:     $\mathrm{mdepth}$ – int64int32nag_int scalar

Default: $0$

$K$, the maximum depth for the iterative process, which in turn puts an upper limit on the number of change points with $m\le 2^K$.

If $K\le 0$ then no limit is put on the depth of the iterative process and no upper limit is put on the number of change points.

3:     $\mathrm{user}$ – Any MATLAB object

user is not used by nag_tsa_cp_binary_user (g13ne), but is passed to chgpfn. Note that for large objects it may be more efficient to use a global variable which is accessible from the m-files than to use user.

Output Parameters

1:     $\mathrm{tau}\left(\mathbf{ntau}\right)$ – int64int32nag_int array

The dimension of the array tau will be $\mathbf{ntau}$

The location of the change points. The $i$th segment is defined by $y_{\left({\tau }_{i-1}+1\right)}$ to $y_{{\tau }_i}$, where ${\tau }_0=0$ and ${\tau }_i=\mathbf{tau}\left(i\right),1\le i\le m$.

2:     $\mathrm{user}$ – Any MATLAB object

3:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.

   $\mathbf{ifail}=11$

Constraint: $\mathbf{n}\ge 2$.

   $\mathbf{ifail}=31$

Constraint: $\mathbf{minss}\ge 2$.

   $\mathbf{ifail}=51$

User requested termination by setting .

W  $\mathbf{ifail}=52$

User requested a segment to be skipped by setting .

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Example

Open in the MATLAB editor: g13ne_example

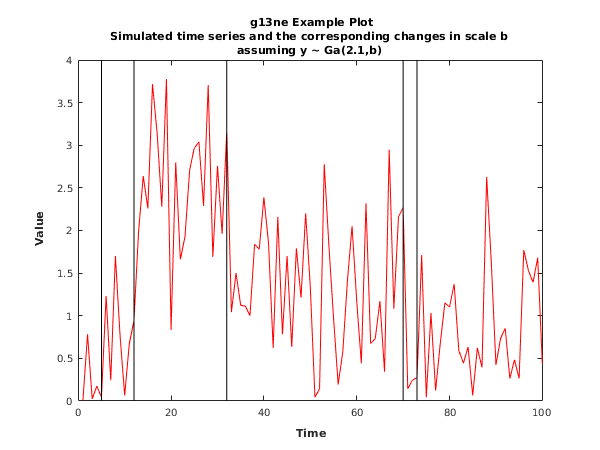
function g13ne_example


fprintf('g13ne example results\n\n');

% Input series
y = [ 0.00; 0.78; 0.02; 0.17; 0.04; 1.23; 0.24; 1.70; 0.77; 0.06;
      0.67; 0.94; 1.99; 2.64; 2.26; 3.72; 3.14; 2.28; 3.78; 0.83;
      2.80; 1.66; 1.93; 2.71; 2.97; 3.04; 2.29; 3.71; 1.69; 2.76;
      1.96; 3.17; 1.04; 1.50; 1.12; 1.11; 1.00; 1.84; 1.78; 2.39;
      1.85; 0.62; 2.16; 0.78; 1.70; 0.63; 1.79; 1.21; 2.20; 1.34;
      0.04; 0.14; 2.78; 1.83; 0.98; 0.19; 0.57; 1.41; 2.05; 1.17;
      0.44; 2.32; 0.67; 0.73; 1.17; 0.34; 2.95; 1.08; 2.16; 2.27;
      0.14; 0.24; 0.27; 1.71; 0.04; 1.03; 0.12; 0.67; 1.15; 1.10;
      1.37; 0.59; 0.44; 0.63; 0.06; 0.62; 0.39; 2.63; 1.63; 0.42;
      0.73; 0.85; 0.26; 0.48; 0.26; 1.77; 1.53; 1.39; 1.68; 0.43];

% Shape parameter used in the cost function
a = 2.1;

% Length of the input series
n = int64(numel(y));

% Need some persisteny workspace in the user function
work = zeros(2*n,1);

% The input series, workspace and shape parameter
% constitute the information that needs to be passed to the
% costfun, so pack them together into a cell array which will
% get passed through the NAG function
user = {y; a; work};

% Penalty term
beta = 3.4;

% Drop small regions
minss = int64(3);

[tau] = g13ne(n,beta,@chgpfn,'minss',minss,'user',user);

% Print the results
fprintf('  -- Change Points --\n');
fprintf('  Number     Position\n');
fprintf(' =====================\n');
for i = 1:numel(tau)
  fprintf(' %4d       %6d\n', i, tau(i));
end

% Plot the results
fig1 = figure;

% Plot the original series
plot(y,'Color','red');

% Mark the change points, drop the last one as it is always
% at the end of the series
xpos = transpose(double(tau(1:end-1))*ones(1,2));
ypos = diag(ylim)*ones(2,numel(tau)-1);
line(xpos,ypos,'Color','black');

% Add labels and titles
title({'{\bf g13ne Example Plot}',
       'Simulated time series and the corresponding changes in scale b',
       'assuming y ~ Ga(2.1,b)'});
xlabel('{\bf Time}');
ylabel('{\bf Value}');



function [v,cost,user,info] = chgpfn(side,u,w,minss,user,info)
  % Function to calculate a proposed change point and associated cost
  % The cost is based on the likelihood of the gamma distribution
  y = user{1};
  a = user{2};
  work = user{3};

  % Calculate the first and last positions for potential change
  % points, conditional on the fact that each sub-segment must be
  % at least minss wide
  floc = u + minss - 1;
  lloc = w - minss;
  
  % In order to calculate the cost of having a change point at i, we
  % need to calculate C(y(floc:i)) and C(y(i+1:lloc)), where C(.) is
  % the cost function (based on the gamma distribution in this example).
  % Rather than calculate these values at each call to chgpfn we store
  % the values in work for later use

  % If side = 1 (i.e. we are working with a left hand sub-segment),
  % we already have C(y(floc:i)) for this value of floc, so only need
  % to calculate C(y(i+1:lloc)), similarly when side = 2 we only need
  % to calculate C(y(floc:i))
  % When side = -1, we need the cost of the full segment, which we do
  % in a forwards manner (calculating C(y(floc:i)) in the process), so
  % when side = 0 we only need to calculate C(y(i:1:lloc))

  % Get the intermediate costs
  ys = 0;
  dn = 0;
  if (side==0 | side==1)
    % work(2*i) = C(y(i+1:w))
    for i = w:-1:floc + 1
      dn = dn + 1;
      tmp = dn*a;
      ys = ys + y(i);
      work(2*i-2) = 2.0*tmp*(log(ys)-log(tmp));
    end

    % make sure we return the updated values of work
    user = {y; a; work};

  else
    % work(2*i-1) = C(y(u:i))
    if (side==-1)
      li = w;
    else
      li = lloc;
    end
    for i = u:li
      dn = dn + 1;
      tmp = dn*a;
      ys = ys + y(i);
      work(2*i-1) = 2.0*tmp*(log(ys)-log(tmp));
    end

    % make sure we return the updated values of work
    user = {y; a; work};
  end

  v = int64(0);
  cost = zeros(3,1);
  if (side>=0)
    % Need to find a potential change point
    v = int64(0);
    cost(1) = 0;

    % Loop over all possible change point locations
    for i = floc:lloc
      this_cost = work(2*i-1) + work(2*i);

      if (this_cost<cost(1) | v==0)
        % Update the proposed change point location
        v = int64(i);
        cost(1) = this_cost;
        cost(2) = work(2*i-1);
        cost(3) = work(2*i);
      end
    end

  else
    % Need to calculate the cost for the full segment
    cost(1) = work(2*w-1);

  % No need to populate the rest of COST or V
  end

  % Set info nonzero to terminate execution for any reason
  info = int64(0);

g13ne example results

  -- Change Points --
  Number     Position
 =====================
    1            5
    2           12
    3           32
    4           70
    5           73
    6          100