PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_tsa_kalman_unscented_state_revcom (g13ej)
Purpose
nag_tsa_kalman_unscented_state_revcom (g13ej) applies the Unscented Kalman Filter to a nonlinear state space model, with additive noise.
nag_tsa_kalman_unscented_state_revcom (g13ej) uses reverse communication for evaluating the nonlinear functionals of the state space model.
Syntax
[
irevcm,
x,
st,
xt,
icomm,
rcomm,
ifail] = g13ej(
irevcm,
y,
lx,
ly,
x,
st,
xt,
fxt,
icomm,
rcomm, 'mx',
mx, 'my',
my, 'ropt',
ropt)
[
irevcm,
x,
st,
xt,
icomm,
rcomm,
ifail] = nag_tsa_kalman_unscented_state_revcom(
irevcm,
y,
lx,
ly,
x,
st,
xt,
fxt,
icomm,
rcomm, 'mx',
mx, 'my',
my, 'ropt',
ropt)
Description
nag_tsa_kalman_unscented_state_revcom (g13ej) applies the Unscented Kalman Filter (UKF), as described in
Julier and Uhlmann (1997b) to a nonlinear state space model, with additive noise, which, at time
, can be described by:
where
represents the unobserved state vector of length
and
the observed measurement vector of length
. The process noise is denoted
, which is assumed to have mean zero and covariance structure
, and the measurement noise by
, which is assumed to have mean zero and covariance structure
.
Unscented Kalman Filter Algorithm
Given
, an initial estimate of the state and
and initial estimate of the state covariance matrix, the UKF can be described as follows:
| (a) |
Generate a set of sigma points (see section Sigma Points):
|
| (b) |
Evaluate the known model function :
The function is assumed to accept the matrix, and return an matrix, . The columns of both and correspond to different possible states. The notation is used to denote the th column of , hence the result of applying to the th possible state. |
| (c) |
Time Update:
|
| (d) |
Redraw another set of sigma points (see section Sigma Points):
|
| (e) |
Evaluate the known model function :
The function is assumed to accept the matrix, and return an matrix, . The columns of both and correspond to different possible states. As above is used to denote the th column of . |
| (f) |
Measurement Update:
|
Here
is the Kalman gain matrix,
is the estimated state vector at time
and
the corresponding covariance matrix. Rather than implementing the standard UKF as stated above
nag_tsa_kalman_unscented_state_revcom (g13ej) uses the square-root form described in the
Haykin (2001).
Sigma Points
A nonlinear state space model involves propagating a vector of random variables through a nonlinear system and we are interested in what happens to the mean and covariance matrix of those variables. Rather than trying to directly propagate the mean and covariance matrix, the UKF uses a set of carefully chosen sample points, referred to as sigma points, and propagates these through the system of interest. An estimate of the propagated mean and covariance matrix is then obtained via the weighted sample mean and covariance matrix.
For a vector of
random variables,
, with mean
and covariance matrix
, the sigma points are usually constructed as:
When calculating the weighted sample mean and covariance matrix two sets of weights are required, one used when calculating the weighted sample mean, denoted
and one used when calculated the weighted sample covariance matrix, denoted
. The weights and multiplier,
, are constructed as follows:
where, usually
and
and
are constants. The total number of sigma points,
, is given by
. The constant
is usually set to somewhere in the range
and for a Gaussian distribution, the optimal values of
and
are
and
respectively.
Rather than redrawing another set of sigma points in
(d) of the UKF an alternative method can be used where the sigma points used in
(a) are augmented to take into account the process noise. This involves replacing equation
(5) with:
Augmenting the sigma points in this manner requires setting to (and hence to ) and recalculating the weights. These new values are then used for the rest of the algorithm. The advantage of augmenting the sigma points is that it keeps any odd-moments information captured by the original propagated sigma points, at the cost of using a larger number of points.
References
Haykin S (2001) Kalman Filtering and Neural Networks John Wiley and Sons
Julier S J (2002) The scaled unscented transformation Proceedings of the 2002 American Control Conference (Volume 6) 4555–4559
Julier S J and Uhlmann J K (1997a) A consistent, debiased method for converting between polar and Cartesian coordinate systems Proceedings of AeroSense97, International Society for Optics and Phonotonics 110–121
Julier S J and Uhlmann J K (1997b) A new extension of the Kalman Filter to nonlinear systems International Symposium for Aerospace/Defense, Sensing, Simulation and Controls (Volume 3) 26
Parameters
Note: this function uses
reverse communication. Its use involves an initial entry, intermediate exits and re-entries, and a final exit, as indicated by the argument
irevcm. Between intermediate exits and re-entries,
all arguments other than fxt must remain unchanged.
Compulsory Input Parameters
- 1:
– int64int32nag_int scalar
-
On initial entry: must be set to
or
.
If , it is assumed that , otherwise it is assumed that and that nag_tsa_kalman_unscented_state_revcom (g13ej) has been called at least once before at an earlier time step.
On intermediate re-entry:
irevcm must remain unchanged.
Constraint:
, , or .
- 2:
– double array
-
, the observed data at the current time point.
- 3:
– double array
-
The first dimension of the array
lx must be at least
.
The second dimension of the array
lx must be at least
.
, such that
, i.e., the lower triangular part of a Cholesky decomposition of the process noise covariance structure. Only the lower triangular part of
lx is referenced.
If is time dependent, then the value supplied should be for time .
- 4:
– double array
-
The first dimension of the array
ly must be at least
.
The second dimension of the array
ly must be at least
.
, such that
, i.e., the lower triangular part of a Cholesky decomposition of the observation noise covariance structure. Only the lower triangular part of
ly is referenced.
If is time dependent, then the value supplied should be for time .
- 5:
– double array
-
On initial entry: the state vector for the previous time point.
On intermediate re-entry:
x must remain unchanged.
- 6:
– double array
-
The first dimension of the array
st must be at least
.
The second dimension of the array
st must be at least
.
On initial entry:
, such that
, i.e., the lower triangular part of a Cholesky decomposition of the state covariance matrix at the previous time point. Only the lower triangular part of
st is referenced.
On intermediate re-entry:
st must remain unchanged.
- 7:
– double array
-
The first dimension,
, of the array
xt must satisfy
- if or , ;
- otherwise .
The second dimension of the array
xt must be at least
if
or
, and at least
otherwise.
On initial entry: need not be set.
On intermediate re-entry:
xt must remain unchanged.
- 8:
– double array
-
The first dimension,
, of the array
fxt must satisfy
- if , ;
- if , ;
- otherwise .
The second dimension of the array
fxt must be at least
if
or
, and at least
otherwise.
On initial entry: need not be set.
On intermediate re-entry:
when
, otherwise
for the values of
and
held in
xt.
For the th sigma point the value for the th parameter should be held in
, for . When , and when , .
- 9:
– int64int32nag_int array
The dimension of the array
must be at least
if , or , and at least otherwise
- 10:
– double array
The dimension of the array
must be at least
if , or , and at least otherwise
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the array
x and the first dimension of the arrays
st,
lx and the second dimension of the array
lx. (An error is raised if these dimensions are not equal.)
, the number of state variables.
Constraint:
.
- 2:
– int64int32nag_int scalar
-
Default:
the dimension of the array
y and the first dimension of the array
ly and the second dimension of the array
ly. (An error is raised if these dimensions are not equal.)
, the number of observed variables.
Constraint:
.
- 3:
– double array
-
Optional arguments. The default value will be used for
if
. Setting
will use the default values for all optional arguments and
ropt need not be set.
- If set to then the second set of sigma points are redrawn, as given by equation (5). If set to then the second set of sigma points are generated via augmentation, as given by equation (13).
Default is for the sigma points to be redrawn (i.e., )
- , value of used when constructing the first set of sigma points, .
Defaults to .
- , value of used when constructing the first set of sigma points, .
Defaults to .
- , value of used when constructing the first set of sigma points, .
Defaults to .
- Value of used when constructing the second set of sigma points, .
Defaults to when and the second set of sigma points are augmented and otherwise.
- Value of used when constructing the second set of sigma points, .
Defaults to .
- Value of used when constructing the second set of sigma points, .
Defaults to .
Constraints:
- or ;
- ;
- when and the second set of sigma points are augmented, otherwise ;
- , for .
Output Parameters
- 1:
– int64int32nag_int scalar
-
On intermediate exit:
or
. The value of
irevcm specifies what intermediate values are returned by this function and what values the calling program must assign to arguments of
nag_tsa_kalman_unscented_state_revcom (g13ej) before re-entering the routine. Details of the output and required input are given in the individual argument descriptions.
On final exit:
- 2:
– double array
-
On intermediate exit:
when
- x is unchanged.
- .
On final exit: the updated state vector.
- 3:
– double array
-
The first dimension of the array
st will be
.
The second dimension of the array
st will be
.
On intermediate exit:
when
- st is unchanged.
- , the lower triangular part of a Cholesky factorization of .
On final exit: , the lower triangular part of a Cholesky factorization of the updated state covariance matrix.
- 4:
– double array
-
The second dimension of the array
xt will be
.
On intermediate exit:
when
, otherwise
.
For the th sigma point, the value for the th parameter is held in
, for and .
On final exit: the contents of
xt are undefined.
- 5:
– int64int32nag_int array
-
.
On intermediate exit:
icomm is used for storage between calls to
nag_tsa_kalman_unscented_state_revcom (g13ej).
.
On final exit:
icomm is not defined.
- 6:
– double array
-
.
On intermediate exit:
rcomm is used for storage between calls to
nag_tsa_kalman_unscented_state_revcom (g13ej).
.
On final exit:
rcomm is not defined.
- 7:
– int64int32nag_int scalar
On final exit:
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
Constraint: , , or .
-
-
Constraint: .
-
-
mx has changed between calls.
-
-
Constraint: .
-
-
my has changed between calls.
-
-
Constraint: or .
-
-
Constraint: .
-
-
Constraint: .
-
-
Constraint: or .
-
-
Constraint: .
-
-
Constraint: .
-
-
Constraint: .
-
-
icomm has been corrupted between calls.
-
-
rcomm has been corrupted between calls.
-
-
A weight was negative and it was not possible to downdate the Cholesky factorization.
-
-
Unable to calculate the Kalman gain matrix.
-
-
Unable to calculate the Cholesky factorization of the updated state covariance matrix.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
Not applicable.
Further Comments
None.
Example
This example implements the following nonlinear state space model, with the state vector
and state update function
given by:
where
and
are known constants and
and
are time-dependent knowns. The measurement vector
and measurement function
is given by:
where
and
are known constants. The initial values,
and
, are given by
and the Cholesky factorizations of the error covariance matrices,
and
by
Open in the MATLAB editor:
g13ej_example
function g13ej_example
fprintf('g13ej example results\n\n');
lx = 0.1 * eye(3);
ly = 0.01 * eye(2);
ix = zeros(size(lx,1),1);
x = ix;
st = 0.1 * eye(3);
r = 3;
d = 4;
Delta = 5.814;
A = 0.464;
y = [ 5.262 5.923; 4.347 5.783; 3.818 6.181;
2.706 0.085; 1.878 0.442; 0.684 0.836;
0.752 1.300; 0.464 1.700; 0.597 1.781;
0.842 2.040; 1.412 2.286; 1.527 2.820;
2.399 3.147; 2.661 3.569; 3.327 3.659];
ntime = size(y,1);
phi_r = ones(ntime,1) * 0.4;
phi_l = ones(ntime,1) * 0.1;
mx = numel(x);
my = size(ly,1);
cx = zeros(mx,ntime);
irevcm = int64(0);
xt = [];
fxt = [];
icomm = int64([]);
rcomm = [];
for t = 1:ntime
y_t = y(t,:);
phi_rt = phi_r(t);
phi_lt = phi_l(t);
while true
[irevcm,x,st,xt,icomm,rcomm,ifail] = ...
g13ej( ...
irevcm,y_t,lx,ly, x,st,xt,fxt,icomm,rcomm);
switch irevcm
case 1
fxt = f(xt,r,d,phi_rt,phi_lt);
case 2
fxt = h(xt,Delta,A);
otherwise
break;
end
end
cx(:,t) = x(:);
end
ttext = [' Time ' blanks(ceil((11*mx- 16)/2)) ' Estimate of State' ...
blanks(ceil((11*mx -16)/2))];
fprintf('%s\n',ttext);
ttext(:) = '-';
fprintf('%s\n',ttext);
for t = 1:ntime
fprintf(' %3d ', t);
fprintf(' %10.3f', cx(1:mx,t));
fprintf('\n');
end
fprintf('\nEstimate of Cholesky Factorisation of the State\n');
fprintf('Covariance Matrix at the Last Time Point\n');
for i=1:mx
for j=1:i
fprintf(' %10.2e',st(i,j));
end
fprintf('\n');
end
fig1 = figure;
pos_no_slippage(:,1) = ix;
rot_mat = [r/2 r/2; 0 0;r/d -r/d];
for t=1:ntime
v_r = rot_mat * [phi_r(t); phi_l(t)];
theta = pos_no_slippage(3,t);
T = [cos(theta) -sin(theta) 0; sin(theta) cos(theta) 0; 0 0 1];
pos_no_slippage(:,t+1) = pos_no_slippage(:,t) + T*v_r;
end
b = -cos(A) / sin(A);
a = Delta * (sin(A) + cos(A)^2/sin(A));
pos_actual = [0.000 0.617 1.590 2.192 ...
3.238 3.947 4.762 4.734 ...
4.529 3.955 3.222 2.209 ...
2.047 1.137 0.903 0.443;
0.000 0.000 0.101 0.079 ...
0.474 0.908 1.947 1.850 ...
2.904 3.757 4.675 5.425 ...
5.492 5.362 5.244 4.674;
0.000 0.103 0.036 0.361 ...
0.549 0.906 1.299 1.763 ...
2.164 2.245 2.504 2.749 ...
3.284 3.610 4.033 4.123];
h(1) = plot_robot(pos_no_slippage,'s','green','green');
hold on
h(2) = plot_robot(pos_actual,'c','red','red');
h(3) = plot_robot([zeros(3,1) cx],'c','blue','none');
hold off
yl = ylim;
line([(yl(1) - a)/b (yl(2) - a) / b],yl,'Color','black');
xlim([-0.5 7]);
title({'{\bf g13ej Example Plot}',
'Illustration of Position and Orientation',
' of Hypothetical Robot'});
label = ['Initial' 'Actual' 'Updated'];
h(4) = legend(h,'Initial','Actual','Updated','Location','NorthEast');
set(h(4),'FontSize',get(h(4),'FontSize')*0.8);
text(4.6,3.9,'Wall','Rotation',-63);
function [fxt] = f(xt,r,d,phi_rt,phi_lt)
fxt = zeros(size(xt));
t1 = 0.5*r*(phi_rt+phi_lt);
t3 = (r/d)*(phi_rt-phi_lt);
fxt(1,:) = xt(1,:) + cos(xt(3,:))*t1;
fxt(2,:) = xt(2,:) + sin(xt(3,:))*t1;
fxt(3,:) = xt(3,:) + t3;
function [hyt] = h(yt,Delta,A)
hyt(1,:) = Delta - yt(1,:)*cos(A) - yt(2,:)*sin(A);
hyt(2,:) = yt(3,:) - A;
hyt(2,(hyt(2,:) < 0)) = hyt(2,(hyt(2,:) < 0)) + 2 * pi;
function [h] = plot_robot(x,symbol,colour,fill)
alen = 0.3;
h = scatter(x(1,:),x(2,:),60,colour,symbol,'MarkerFaceColor',fill);
aend = [x(1,:)+alen*cos(x(3,:)); x(2,:)+alen*sin(x(3,:))];
line([x(1,:); aend(1,:)],[x(2,:); aend(2,:)],'Color',colour);
g13ej example results
Time Estimate of State
--------------------------------------------
1 0.664 -0.092 0.104
2 1.598 0.081 0.314
3 2.128 0.213 0.378
4 3.134 0.674 0.660
5 3.809 1.181 0.906
6 4.730 2.000 1.298
7 4.429 2.474 1.762
8 4.357 3.246 2.162
9 3.907 3.852 2.246
10 3.360 4.398 2.504
11 2.552 4.741 2.750
12 2.191 5.193 3.281
13 1.309 5.018 3.610
14 1.071 4.894 4.031
15 0.618 4.322 4.124
Estimate of Cholesky Factorisation of the State
Covariance Matrix at the Last Time Point
1.92e-01
-3.82e-01 2.22e-02
1.58e-06 2.23e-07 9.95e-03
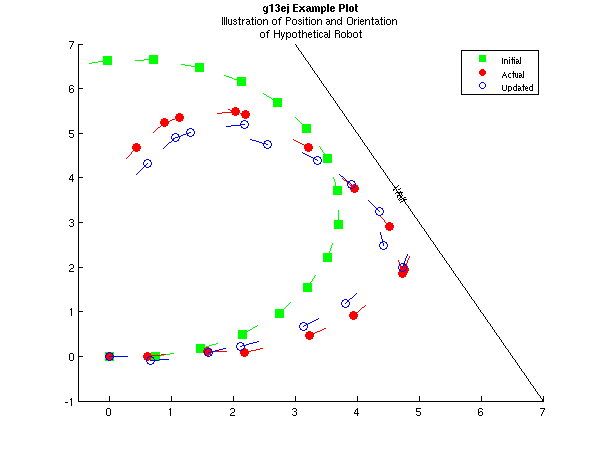
The example described above can be thought of as relating to the movement of a hypothetical robot. The unknown state, , is the position of the robot (with respect to a reference frame) and facing, with giving the and coordinates and the angle (with respect to the -axis) that the robot is facing. The robot has two drive wheels, of radius on an axle of length . During time period the right wheel is believed to rotate at a velocity of and the left at a velocity of . In this example, these velocities are fixed with and . The state update function, , calculates where the robot should be at each time point, given its previous position. However, in reality, there is some random fluctuation in the velocity of the wheels, for example, due to slippage. Therefore the actual position of the robot and the position given by equation will differ.
In the area that the robot is moving there is a single wall. The position of the wall is known and defined by its distance, , from the origin and its angle, , from the -axis. The robot has a sensor that is able to measure , with being the distance to the wall and the angle to the wall. The measurement function gives the expected distance and angle to the wall if the robot's position is given by . Therefore the state space model allows the robot to incorporate the sensor information to update the estimate of its position.
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015
