NAG Toolbox: nag_correg_lars (g02ma)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{mtype}$ – int64int32nag_int scalar

Indicates the type of model to fit.

$\mathbf{mtype}=1$

LARS is performed.

$\mathbf{mtype}=2$

Forward linear stagewise regression is performed.

$\mathbf{mtype}=3$

LASSO model is fit.

$\mathbf{mtype}=4$

A positive LASSO model is fit.

Constraint: $\mathbf{mtype}=1$, $2$, $3$ or $4$.

2:     $\mathrm{m}$ – int64int32nag_int scalar

$m$, the total number of independent variables$\mathbf{m}=p$ when all variables are included.

Constraint: $\mathbf{m}\ge 1$.

3:     $\mathrm{d}\left(\mathit{ldd},:\right)$ – double array

The first dimension of the array d must be at least $\mathbf{n}$.

The second dimension of the array d must be at least $\mathbf{m}$.

$D$, the data, which along with pred and isx, defines the design matrix $X$. The $\mathit{i}$th observation for the $\mathit{j}$th variable must be supplied in $\mathbf{d}\left(\mathit{i},\mathit{j}\right)$, for $\mathit{i}=1,2,\dots ,\mathbf{n}$ and $\mathit{j}=1,2,\dots ,\mathbf{m}$.

4:     $\mathrm{y}\left(\mathbf{n}\right)$ – double array

$y$, the observations on the dependent variable.

Optional Input Parameters

1:     $\mathrm{pred}$ – int64int32nag_int scalar

Default: $\mathbf{pred}=3$

Indicates the type of data preprocessing to perform on the independent variables supplied in d to comply with the standardized form of the design matrix.

$\mathbf{pred}=0$

No preprocessing is performed.

$\mathbf{pred}=1$

Each of the independent variables, $x_{\mathit{j}}$, for $\mathit{j}=1,2,\dots ,p$, are mean centered prior to fitting the model. The means of the independent variables, $\stackrel{-}{x}$, are returned in b, with ${\stackrel{-}{x}}_{\mathit{j}}=\mathbf{b}\left(\mathit{j},\mathbf{nstep}+2\right)$, for $\mathit{j}=1,2,\dots ,p$.

$\mathbf{pred}=2$

Each independent variable is normalized, with the $j$th variable scaled by $1/\sqrt{x_j^{\mathrm{T}}{x}_j}$. The scaling factor used by variable $j$ is returned in $\mathbf{b}\left(\mathit{j},\mathbf{nstep}+1\right)$.

$\mathbf{pred}=3$

As $\mathbf{pred}=1$ and $2$, all of the independent variables are mean centered prior to being normalized.

Constraint: $\mathbf{pred}=0$, $1$, $2$ or $3$.

2:     $\mathrm{prey}$ – int64int32nag_int scalar

Default: $\mathbf{prey}=1$

Indicates the type of data preprocessing to perform on the dependent variable supplied in y.

$\mathbf{prey}=0$

No preprocessing is performed, this is equivalent to setting $\alpha =0$.

$\mathbf{prey}=1$

The dependent variable, $y$, is mean centered prior to fitting the model, so $\alpha =\stackrel{-}{y}$. Which is equivalent to fitting a non-penalized intercept to the model and the degrees of freedom etc. are adjusted accordingly.

The value of $\alpha$ used is returned in $\mathbf{fitsum}\left(1,\mathbf{nstep}+1\right)$.

Constraint: $\mathbf{prey}=0$ or $1$.

3:     $\mathrm{n}$ – int64int32nag_int scalar

Default: the dimension of the array y and the first dimension of the array d. (An error is raised if these dimensions are not equal.)

$n$, the number of observations.

Constraint: $\mathbf{n}\ge 1$.

4:     $\mathrm{isx}\left(\mathbf{lisx}\right)$ – int64int32nag_int array

Indicates which independent variables from d will be included in the design matrix, $X$.

If isx is not supplied, all variables are included in the design matrix.

Otherwise, for $\mathit{j}=1,2,\dots ,\mathbf{m}$ when $\mathbf{isx}\left(j\right)$ must be set as follows:

$\mathbf{isx}\left(j\right)=1$

To indicate that the $j$th variable, as supplied in d, is included in the design matrix;

$\mathbf{isx}\left(j\right)=0$

To indicated that the $j$th variable, as supplied in d, is not included in the design matrix;

and $p={\displaystyle \sum _{\mathit{j}=1}^m}\mathbf{isx}\left(\mathit{j}\right)$

Constraint: $\mathbf{isx}\left(\mathit{j}\right)=0$ or $1$ and at least one value of $\mathbf{isx}\left(\mathit{j}\right)\ne 0$, for $\mathit{j}=1,2,\dots ,\mathbf{m}$.

5:     $\mathrm{mnstep}$ – int64int32nag_int scalar

Default:

• if $\mathbf{mtype}=1$, $\mathbf{mnstep}=\mathbf{m}$;
• otherwise $\mathbf{mnstep}=200\times \mathbf{m}$.

The maximum number of steps to carry out in the model fitting process.

If $\mathbf{mtype}=1$, i.e., a LARS is being performed, the maximum number of steps the algorithm will take is $\min \left(p,n\right)$ if $\mathbf{prey}=0$, otherwise $\min \left(p,n-1\right)$.

If $\mathbf{mtype}=2$, i.e., a forward linear stagewise regression is being performed, the maximum number of steps the algorithm will take is likely to be several orders of magnitude more and is no longer bound by $p$ or $n$.

If $\mathbf{mtype}=3$ or $4$, i.e., a LASSO or positive LASSO model is being fit, the maximum number of steps the algorithm will take lies somewhere between that of the LARS and forward linear stagewise regression, again it is no longer bound by $p$ or $n$.

Constraint: $\mathbf{mnstep}\ge 1$.

6:     $\mathrm{ropt}\left(\mathbf{lropt}\right)$ – double array

Optional parameters to control various aspects of the LARS algorithm.

The default value will be used for $\mathbf{ropt}\left(i\right)$ if $\mathbf{lropt}<i$. The default value will also be used if an invalid value is supplied for a particular argument, for example, setting $\mathbf{ropt}\left(i\right)=-1$ will use the default value for argument $i$.

$\mathbf{ropt}\left(1\right)$

The minimum step size that will be taken.

Default is $100\times \mathit{eps}$ is used, where $\mathit{eps}$ is the machine precision returned by nag_machine_precision (x02aj).

$\mathbf{ropt}\left(2\right)$

General tolerance, used amongst other things, for comparing correlations.

Default is $\mathbf{ropt}\left(1\right)$.

$\mathbf{ropt}\left(3\right)$

If set to $1$, parameter estimates are rescaled before being returned.

If set to $0$, no rescaling is performed.

This argument has no effect when $\mathbf{pred}=0$ or $1$.

Default is for the parameter estimates to be rescaled.

$\mathbf{ropt}\left(4\right)$

If set to $1$, it is assumed that the model contains an intercept during the model fitting process and when calculating the degrees of freedom.

If set to $0$, no intercept is assumed.

This has no effect on the amount of preprocessing performed on y.

Default is to treat the model as having an intercept when $\mathbf{prey}=1$ and as not having an intercept when $\mathbf{prey}=0$.

$\mathbf{ropt}\left(5\right)$

As implemented, the LARS algorithm can either work directly with $y$ and $X$, or it can work with the cross-product matrices, $X^{\mathrm{T}}y$ and $X^{\mathrm{T}}X$. In most cases it is more efficient to work with the cross-product matrices. This flag allows you direct control over which method is used, however, the default value will usually be the best choice.

If $\mathbf{ropt}\left(5\right)=1$, $y$ and $X$ are worked with directly.

If $\mathbf{ropt}\left(5\right)=0$, the cross-product matrices are used.

Default is $1$ when $p\ge 500$ and $n<p$ and $0$ otherwise.

Constraints:

• $\mathbf{ropt}\left(1\right)>\mathit{machine precision}$;
• $\mathbf{ropt}\left(2\right)>\mathit{machine precision}$;
• $\mathbf{ropt}\left(3\right)=0$ or $1$;
• $\mathbf{ropt}\left(4\right)=0$ or $1$;
• $\mathbf{ropt}\left(5\right)=0$ or $1$.

Output Parameters

1:     $\mathrm{b}\left(\mathit{p},:\right)$ – double array

The second dimension of the array b will be $\mathbf{nstep}+2$.

Note: nstep is equal to $K$, the actual number of steps carried out in the model fitting process. See Description for further information.

$\beta$ the parameter estimates, with $\mathbf{b}\left(j,k\right)={\beta }_{kj}$, the parameter estimate for the $j$th variable, $j=1,2,\dots ,p$ at the $k$th step of the model fitting process, $k=1,2,\dots ,\mathbf{nstep}$.

By default, when $\mathbf{pred}=2$ or $3$ the parameter estimates are rescaled prior to being returned. If the parameter estimates are required on the normalized scale, then this can be overridden via ropt.

The values held in the remaining part of b depend on the type of preprocessing performed.

If $\mathbf{pred}=0$,

$\begin{array}{lll}\mathbf{b}\left(j,\mathbf{nstep}+1\right)& =& 1\\ \mathbf{b}\left(j,\mathbf{nstep}+2\right)& =& 0\end{array}$

If $\mathbf{pred}=1$,

$\begin{array}{lll}\mathbf{b}\left(j,\mathbf{nstep}+1\right)& =& 1\\ \mathbf{b}\left(j,\mathbf{nstep}+2\right)& =& {\stackrel{-}{x}}_j\end{array}$

If $\mathbf{pred}=2$,

$\begin{array}{lll}\mathbf{b}\left(j,\mathbf{nstep}+1\right)& =& 1/\sqrt{x_j^{\mathrm{T}}{x}_j}\\ \mathbf{b}\left(j,\mathbf{nstep}+2\right)& =& 0\end{array}$

If $\mathbf{pred}=3$,

$\begin{array}{lll}\mathbf{b}\left(j,\mathbf{nstep}+1\right)& =& 1/\sqrt{{\left(x_j-{\stackrel{-}{x}}_j\right)}^{\mathrm{T}}\left(x_j-{\stackrel{-}{x}}_j\right)}\\ \mathbf{b}\left(j,\mathbf{nstep}+2\right)& =& {\stackrel{-}{x}}_j\end{array}$

for $j=1,2,\dots ,p$.

The number of parameter estimates, $p$, is the number of columns in d when isx is not supplied, i.e., $p=\mathbf{m}$. Otherwise $p$ is the number of nonzero values in isx.

2:     $\mathrm{fitsum}\left(6,\mathbf{mnstep}+1\right)$ – double array

The second dimension of the array fitsum will be $\mathbf{nstep}+1$.

Note: nstep is equal to $K$, the actual number of steps carried out in the model fitting process. See Description for further information.

Summaries of the model fitting process. When $k=1,2,\dots ,\mathbf{nstep}$,

$\mathbf{fitsum}\left(1,k\right)$

${‖{\beta }_k‖}_1$, the sum of the absolute values of the parameter estimates for the $k$th step of the modelling fitting process. If $\mathbf{pred}=2$ or $3$, the scaled parameter estimates are used in the summation.

$\mathbf{fitsum}\left(2,k\right)$

${\mathrm{RSS}}_k$, the residual sums of squares for the $k$th step, where ${\mathrm{RSS}}_k={‖y-X^{\mathrm{T}}{\beta }_k‖}^2$.

$\mathbf{fitsum}\left(3,k\right)$

${\nu }_k$, approximate degrees of freedom for the $k$th step.

$\mathbf{fitsum}\left(4,k\right)$

$C_p^{\left(k\right)}$, a $C_p$-type statistic for the $k$th step, where $C_p^{\left(k\right)}=\frac{{\mathrm{RSS}}_k}{{\sigma }^2}-n+2{\nu }_k$.

$\mathbf{fitsum}\left(5,k\right)$

${\hat{C}}_k$, correlation between the residual at step $k-1$ and the most correlated variable not yet in the active set $\mathcal{A}$, where the residual at step $0$ is $y$.

$\mathbf{fitsum}\left(6,k\right)$

${\hat{\gamma }}_k$, the step size used at step $k$.

In addition

$\mathbf{fitsum}\left(1,\mathbf{nstep}+1\right)$

$\alpha$, with $\alpha =\stackrel{-}{y}$ if $\mathbf{prey}=1$ and $0$ otherwise.

$\mathbf{fitsum}\left(2,\mathbf{nstep}+1\right)$

${\mathrm{RSS}}_0$, the residual sums of squares for the null model, where ${\mathrm{RSS}}_0=y^{\mathrm{T}}y$ when $\mathbf{prey}=0$ and ${\mathrm{RSS}}_0={\left(y-\stackrel{-}{y}\right)}^{\mathrm{T}}\left(y-\stackrel{-}{y}\right)$ otherwise.

$\mathbf{fitsum}\left(3,\mathbf{nstep}+1\right)$

${\nu }_0$, the degrees of freedom for the null model, where ${\nu }_0=0$ if $\mathbf{prey}=0$ and ${\nu }_0=1$ otherwise.

$\mathbf{fitsum}\left(4,\mathbf{nstep}+1\right)$

$C_p^{\left(0\right)}$, a $C_p$-type statistic for the null model, where $C_p^{\left(0\right)}=\frac{{\mathrm{RSS}}_0}{{\sigma }^2}-n+2{\nu }_0$.

$\mathbf{fitsum}\left(5,\mathbf{nstep}+1\right)$

${\sigma }^2$, where ${\sigma }^2=\frac{n-{\mathrm{RSS}}_K}{{\nu }_K}$ and $K=\mathbf{nstep}$.

Although the $C_p$ statistics described above are returned when $\mathbf{ifail}=\mathbf{112}$ they may not be meaningful due to the estimate ${\sigma }^2$ not being based on the saturated model.

3:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.

   $\mathbf{ifail}=11$

Constraint: $\mathbf{mtype}=1$, $2$, $3$ or $4$.

   $\mathbf{ifail}=21$

Constraint: $\mathbf{pred}=0$, $1$, $2$ or $3$.

   $\mathbf{ifail}=31$

Constraint: $\mathbf{prey}=0$ or $1$.

   $\mathbf{ifail}=41$

Constraint: $\mathbf{n}\ge 1$.

   $\mathbf{ifail}=51$

Constraint: $\mathbf{m}\ge 1$.

   $\mathbf{ifail}=81$

Constraint: $\mathbf{isx}\left(i\right)=0$ or $1$ for all $i$.

   $\mathbf{ifail}=82$

On entry, all values of isx are zero.
Constraint: at least one value of isx must be nonzero.

   $\mathbf{ifail}=111$

Constraint: $\mathbf{mnstep}\ge 1$.

W  $\mathbf{ifail}=112$

Fitting process did not finish in mnstep steps. Try increasing the size of mnstep.
All output is returned as documented, up to step mnstep, however, $\sigma$ and the $C_p$ statistics may not be meaningful.

W  $\mathbf{ifail}=161$

${\sigma }^2$ is approximately zero and hence the $C_p$-type criterion cannot be calculated. All other output is returned as documented.

W  $\mathbf{ifail}=162$

${\nu }_K=n$, therefore $\sigma$ has been set to a large value. Output is returned as documented.

W  $\mathbf{ifail}=163$

Degenerate model, no variables added and $\mathbf{nstep}=0$. Output is returned as documented.

   $\mathbf{ifail}=181$

Constraint: $0\le \mathbf{lropt}\le 5$.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Example

Open in the MATLAB editor: g02ma_example

function g02ma_example


fprintf('g02ma example results\n\n');

% Going to be fitting a LAR model via g02ma
mtype = int64(1);

% Independent variables
d = [10.28  1.77  9.69 15.58  8.23 10.44;
      9.08  8.99 11.53  6.57 15.89 12.58;
     17.98 13.10  1.04 10.45 10.12 16.68;
     14.82 13.79 12.23  7.00  8.14  7.79;
     17.53  9.41  6.24  3.75 13.12 17.08;
      7.78 10.38  9.83  2.58 10.13  4.25;
     11.95 21.71  8.83 11.00 12.59 10.52;
     14.60 10.09 -2.70  9.89 14.67  6.49;
      3.63  9.07 12.59 14.09  9.06  8.19;
      6.35  9.79  9.40 12.79  8.38 16.79;
      4.66  3.55 16.82 13.83 21.39 13.88;
      8.32 14.04 17.17  7.93  7.39 -1.09;
     10.86 13.68  5.75 10.44 10.36 10.06;
      4.76  4.92 17.83  2.90  7.58 11.97;
      5.05 10.41  9.89  9.04  7.90 13.12;
      5.41  9.32  5.27 15.53  5.06 19.84;
      9.77  2.37  9.54 20.23  9.33  8.82;
     14.28  4.34 14.23 14.95 18.16 11.03;
     10.17  6.80  3.17  8.57 16.07 15.93;
      5.39  2.67  6.37 13.56 10.68  7.35];

% Dependent variable
y = [-46.47; -35.80; -129.22;  -42.44; -73.51;
     -26.61; -63.90;  -76.73;  -32.64; -83.29;
     -16.31;  -5.82;  -47.75;   18.38; -54.71;
     -55.62; -45.28;  -22.76; -104.32; -55.94];

% g02ma can issue warnings, but return sensible results,
% so save current warning state and turn warnings on
warn_state = nag_issue_warnings();
nag_issue_warnings(true);

[b,fitsum,ifail] = g02ma(mtype,d,y);

% Reset the warning state to its initial value
nag_issue_warnings(warn_state);

% Print the results
ip = size(b,1);
K = size(b,2) - 2;

fprintf('  Step %s Parameter Estimate\n ',repmat(' ',1,max(ip-2,0)*5));
fprintf(repmat('-',1,5+ip*10));
fprintf('\n');
for k = 1:K
  fprintf('  %3d',k);
  for j = 1:ip
    fprintf(' %9.3f',b(j,k));
  end
  fprintf('\n');
end
fprintf('\n');
fprintf(' alpha: %9.3f\n', fitsum(1,K+1));
fprintf('\n');
fprintf('  Step     Sum      RSS       df       Cp       Ck     Step Size\n ');
fprintf(repmat('-',1,64));
fprintf('\n');
for k = 1:K
  fprintf('  %3d %9.3f %9.3f %6.0f  %9.3f %9.3f %9.3f\n', ...
          k,fitsum(1,k),fitsum(2,k),fitsum(3,k), ...
          fitsum(4,k),fitsum(5,k),fitsum(6,k));
end
fprintf('\n');
fprintf(' sigma^2: %9.3f\n', fitsum(5,K+1));

% Plot the parameter estimates
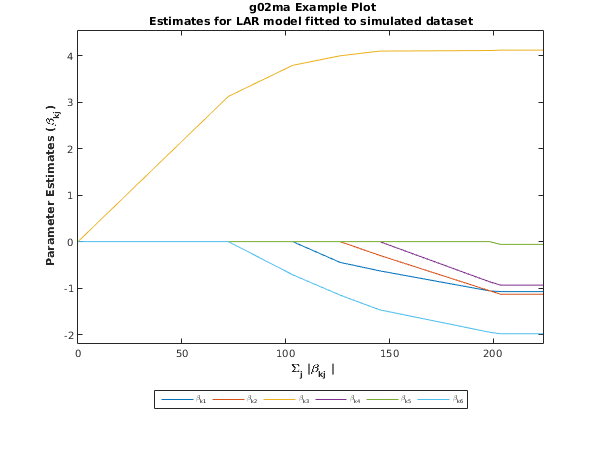
fig1 = figure;

% Extract the sum of the absolute parameter estimates
xpos = transpose(repmat(fitsum(1,1:K),ip,1));

% Extract the parameter estimates
ypos = transpose(b(1:ip,1:K));

% Start both xpos and ypos at zero
xpos = [zeros(1,ip);xpos];
ypos = [zeros(1,ip);ypos];

% Get min and max for X and Y
xmin = min(min(xpos));
xmax = max(max(xpos));
ymin = min(min(ypos));
ymax = max(max(ypos));

% Get a range that is 10% past the data
ext = 1 + [-0.1 0.1];
xrng = [min(xmin*ext),max(xmax*ext)];
yrng = [min(ymin*ext),max(ymax*ext)];

% Extend the end of the lines we plot to cover this range
xpos = [xpos;xrng(2)*ones(1,ip)];
ypos = [ypos;ypos(end,:)];

% Produce the plot
plot(xpos,ypos);

% Change the axis limits
xlim(xrng);
ylim(yrng);

% Add title and labels
title({'{\bf g02ma Example Plot}'; ...
       'Estimates for LAR model fitted to simulated dataset'});
xlabel('{\bf \Sigma_j |\beta_{kj} |}');
ylabel('{\bf Parameter Estimates (\beta_{kj})}');

% Add legend
label = [repmat('\beta_{k',ip,1) num2str(transpose(linspace(1,ip,ip))) ...
         repmat('}',ip,1)];
h = legend(label,'Location','SouthOutside','Orientation','Horizontal');
set(h,'FontSize',get(h,'FontSize')*0.8);

g02ma example results

  Step                      Parameter Estimate
 -----------------------------------------------------------------
    1     0.000     0.000     3.125     0.000     0.000     0.000
    2     0.000     0.000     3.792     0.000     0.000    -0.713
    3    -0.446     0.000     3.998     0.000     0.000    -1.151
    4    -0.628    -0.295     4.098     0.000     0.000    -1.466
    5    -1.060    -1.056     4.110    -0.864     0.000    -1.948
    6    -1.073    -1.132     4.118    -0.935    -0.059    -1.981

 alpha:   -50.037

  Step     Sum      RSS       df       Cp       Ck     Step Size
 ----------------------------------------------------------------
    1    72.446  8929.855      2     13.355   123.227    72.446
    2   103.385  6404.701      3      7.054    50.781    24.841
    3   126.243  5258.247      4      5.286    30.836    16.225
    4   145.277  4657.051      5      5.309    19.319    11.587
    5   198.223  3959.401      6      5.016    12.266    24.520
    6   203.529  3954.571      7      7.000     0.910     2.198

 sigma^2:   304.198