NAG Toolbox: nag_stat_pdf_normal_vector (g01kq)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{ilog}$ – int64int32nag_int scalar

The value of ilog determines whether the logarithmic value is returned in PDF.

$\mathbf{ilog}=0$

$f\left(x_i,{\mu }_i,{\sigma }_i\right)$, the probability density function is returned.

$\mathbf{ilog}=1$

$\log \left(f\left(x_i,{\mu }_i,{\sigma }_i\right)\right)$, the logarithm of the probability density function is returned.

Constraint: $\mathbf{ilog}=0$ or $1$.

2:     $\mathrm{x}\left(\mathbf{lx}\right)$ – double array

$x_i$, the values at which the PDF is to be evaluated with $x_i=\mathbf{x}\left(j\right)$, $j=\left(\left(i-1\right)\mathrm{ mod }\mathbf{lx}\right)+1$, for $i=1,2,\dots ,\max \left(\mathbf{lx},\mathbf{lxstd},\mathbf{lxmu}\right)$.

3:     $\mathrm{xmu}\left(\mathbf{lxmu}\right)$ – double array

${\mu }_i$, the means with ${\mu }_i=\mathbf{xmu}\left(j\right)$, $j=\left(\left(i-1\right)\mathrm{ mod }\mathbf{lxmu}\right)+1$.

4:     $\mathrm{xstd}\left(\mathbf{lxstd}\right)$ – double array

${\sigma }_i$, the standard deviations with ${\sigma }_i=\mathbf{xstd}\left(j\right)$, $j=\left(\left(i-1\right)\mathrm{ mod }\mathbf{lxstd}\right)+1$.

Constraint: $\mathbf{xstd}\left(\mathit{j}\right)\ge 0.0$, for $\mathit{j}=1,2,\dots ,\mathbf{lxstd}$.

Optional Input Parameters

1:     $\mathrm{lx}$ – int64int32nag_int scalar

Default: the dimension of the array x.

The length of the array x.

Constraint: $\mathbf{lx}>0$.

2:     $\mathrm{lxmu}$ – int64int32nag_int scalar

Default: the dimension of the array xmu.

The length of the array xmu.

Constraint: $\mathbf{lxmu}>0$.

3:     $\mathrm{lxstd}$ – int64int32nag_int scalar

Default: the dimension of the array xstd.

The length of the array xstd.

Constraint: $\mathbf{lxstd}>0$.

Output Parameters

1:     $\mathrm{pdf}\left(:\right)$ – double array

The dimension of the array pdf will be $\max \left(\mathbf{lx},\mathbf{lxstd},\mathbf{lxmu}\right)$

$f\left(x_i,{\mu }_i,{\sigma }_i\right)$ or $\log \left(f\left(x_i,{\mu }_i,{\sigma }_i\right)\right)$.

2:     $\mathrm{ivalid}\left(:\right)$ – int64int32nag_int array

The dimension of the array ivalid will be $\max \left(\mathbf{lx},\mathbf{lxstd},\mathbf{lxmu}\right)$

$\mathbf{ivalid}\left(i\right)$ indicates any errors with the input arguments, with

$\mathbf{ivalid}\left(i\right)=0$

No error.

$\mathbf{ivalid}\left(i\right)=1$

${\sigma }_i<0$.

3:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.

W  $\mathbf{ifail}=1$

On entry, at least one value of xstd was invalid.
Check ivalid for more information.

   $\mathbf{ifail}=2$

Constraint: $\mathbf{ilog}=0$ or $1$.

   $\mathbf{ifail}=3$

Constraint: $\mathbf{lx}>0$.

   $\mathbf{ifail}=4$

Constraint: $\mathbf{lxmu}>0$.

   $\mathbf{ifail}=5$

Constraint: $\mathbf{lxstd}>0$.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Example

Open in the MATLAB editor: g01kq_example

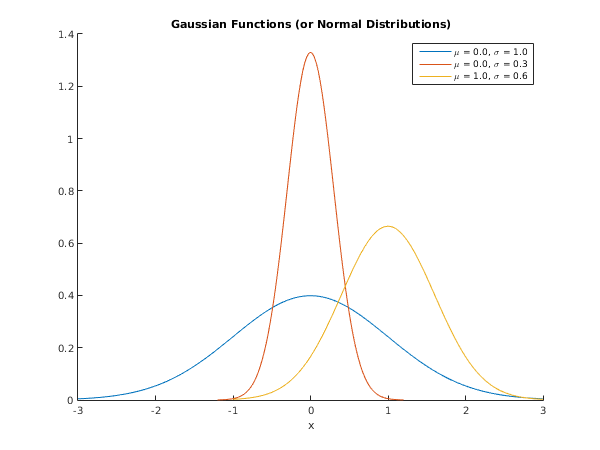
function g01kq_example


fprintf('g01kq example results\n\n');

x =     [1.0, 4.0, 0.1, 1.0];
xmean = [0.0, 2.0, 0.0, 0.0];
xstd =  [1.0, 1.0, 0.01, 10];
ilog = int64(0);
[pdf, ivalid, ifail] = g01kq(ilog, x, xmean, xstd);

fprintf('\n  x             mean          standard      result\n');
fprintf('                              deviation\n');
lx     = numel(x);
lxmean = numel(xmean);
lxstd  = numel(xstd);
len = max ([lx, lxmean, lxstd]);
for i=0:len-1
 fprintf('%13.5e %13.5e %13.5e %13.5e %3d\n', x(mod(i,lx)+1), ...
         xmean(mod(i,lxmean)+1), xstd(mod(i,lxstd)+1), pdf(i+1), ivalid(i+1));
end

g01kq_plot;



function g01kq_plot
 
  fig1 = figure;
  hold on;
  xmean  = [0, 0,   1];
  xstd   = [1, 0.3, 0.6];
  ilog = int64(0);
  x{1} = [-3:0.05:3];
  x{2} = [-1.2:0.025:1.2];
  x{3} = [-1:0.05:3];
  mu = '\mu';
  sigma = '\sigma';
  for i=1:3
    [y{i}, ifail] = g01kq( ...
			   ilog, x{i}, xmean(i), xstd(i));
    plot(x{i},y{i});
    l{i} = sprintf('%s = %3.1f, %s = %3.1f', mu, xmean(i), sigma, xstd(i));
  end
  legend(l);
  xlabel('x');
  title('Gaussian Functions (or Normal Distributions)');
  hold off;

g01kq example results


  x             mean          standard      result
                              deviation
  1.00000e+00   0.00000e+00   1.00000e+00   2.41971e-01   0
  4.00000e+00   2.00000e+00   1.00000e+00   5.39910e-02   0
  1.00000e-01   0.00000e+00   1.00000e-02   7.69460e-21   0
  1.00000e+00   0.00000e+00   1.00000e+01   3.96953e-02   0