NAG Toolbox: nag_sparse_sym_rcm (f11ye)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{icolzp}\left(\mathbf{n}+1\right)$ – int64int32nag_int array

icolzp records the index into irowix which starts each new column.

Constraints:

• $1\le \mathbf{icolzp}\left(\mathit{i}\right)\le \mathbf{nz}+1$, for $\mathit{i}=2,3,\dots ,\mathbf{n}$;
• $\mathbf{icolzp}\left(1\right)=1$;
• $\mathbf{icolzp}\left(\mathbf{n}+1\right)=\mathbf{nz}+1$, where $\mathbf{icolzp}\left(i\right)$ holds the position integer for the starts of the columns in irowix.

2:     $\mathrm{irowix}\left(\mathbf{nz}\right)$ – int64int32nag_int array

The row indices corresponding to the nonzero elements in the matrix $A$.

Constraint: $1\le \mathbf{irowix}\left(\mathit{i}\right)\le \mathbf{n}$, for $\mathit{i}=1,2,\dots ,\mathbf{nz}$.

3:     $\mathrm{lopts}\left(5\right)$ – logical array

The options to be used by nag_sparse_sym_rcm (f11ye).

$\mathbf{lopts}\left(1\right)=\mathit{true}$

Row/column $i$ of the matrix $A$ will only be referenced if $\mathbf{mask}\left(i\right)\ne 0$, otherwise $\mathbf{mask}$ will be ignored.

$\mathbf{lopts}\left(2\right)=\mathit{true}$

The final permutation will not be reversed, that is, the Cuthill–McKee ordering will be returned. The bandwidth of the non-reversed matrix will be the same but the profile will be the same or larger (see Wai-Hung and Sherman (1976)).

$\mathbf{lopts}\left(3\right)=\mathit{true}$

The matrix $A$ will be checked for symmetrical sparsity pattern, otherwise not.

$\mathbf{lopts}\left(4\right)=\mathit{true}$

The bandwidth and profile of the unpermuted matrix will be calculated, otherwise not.

$\mathbf{lopts}\left(5\right)=\mathit{true}$

The bandwidth and profile of the permuted matrix will be calculated, otherwise not.

4:     $\mathrm{mask}\left(:\right)$ – int64int32nag_int array

The dimension of the array mask must be at least $\mathbf{n}$ if $\mathbf{lopts}\left(1\right)=\mathit{true}$, and at least $0$ otherwise

mask is only referenced if $\mathbf{lopts}\left(1\right)$ is true. A value of $\mathbf{mask}\left(i\right)=0$ indicates that the node corresponding to row or column $i$ is not to be referenced. A value of $\mathbf{mask}\left(i\right)\ne 0$ indicates that the node corresponding to row or column $i$ is to be referenced. In particular, rows and columns not referenced will not be permuted.

Optional Input Parameters

1:     $\mathrm{n}$ – int64int32nag_int scalar

Default: $\text{the first dimension of }\mathbf{icolzp}-1$

$n$, the order of the matrix $A$.

Constraint: $\mathbf{n}\ge 1$.

2:     $\mathrm{nz}$ – int64int32nag_int scalar

Default: the dimension of the array irowix.

The number of nonzero elements in the matrix $A$.

Constraint: $\mathbf{nz}\ge 0$.

Output Parameters

1:     $\mathrm{perm}\left(\mathbf{n}\right)$ – int64int32nag_int array

This will contain the permutation vector that describes the permutation matrix $P$ for the reordering of the matrix $A$. The elements of the permutation matrix $P$ are zero except for the unit elements in row $i$ and column $\mathbf{perm}\left(i\right)$, $i=1,2,\dots n$.

2:     $\mathrm{info}\left(4\right)$ – int64int32nag_int array

Statistics about the matrix $A$ and the permuted matrix. The quantities below are calculated using any masking in effect otherwise the value zero is returned.

$\mathbf{info}\left(1\right)$

The bandwidth of the matrix $A$, if $\mathbf{lopts}\left(4\right)=\mathit{true}$.

$\mathbf{info}\left(2\right)$

The profile of the matrix $A$, if $\mathbf{lopts}\left(4\right)=\mathit{true}$.

$\mathbf{info}\left(3\right)$

The bandwidth of the permuted matrix $PA{P}^{\mathrm{T}}$, if $\mathbf{lopts}\left(5\right)=\mathit{true}$.

$\mathbf{info}\left(4\right)$

The profile of the permuted matrix $PA{P}^{\mathrm{T}}$, if $\mathbf{lopts}\left(5\right)=\mathit{true}$.

3:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

   $\mathbf{ifail}=1$

Constraint: $\mathbf{n}\ge 1$.

   $\mathbf{ifail}=2$

Constraint: $\mathbf{nz}\ge 1$.

   $\mathbf{ifail}=3$

Constraint: $1\le \mathbf{irowix}\left(i\right)\le \mathbf{n}$ for all $i$.

   $\mathbf{ifail}=4$

Constraint: $1\le \mathbf{icolzp}\left(i\right)\le \mathbf{nz}$ for all $i$.

   $\mathbf{ifail}=5$

Constraint: $\mathbf{icolzp}\left(1\right)=1$.

Constraint: $\mathbf{icolzp}\left(\mathbf{n}+1\right)=\mathbf{nz}+1$.

   $\mathbf{ifail}=6$

On entry, the matrix $A$ is not symmetric.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Example

Open in the MATLAB editor: f11ye_example

function f11ye_example


fprintf('f11ye example results\n\n');

% Reduce the bandwidth of sparse symmetric matrix A

% Define entries of A using Bucky matrix
A = bucky;
[irow,icol,a] = find(A);

n = int64(size(A,1));
nz = int64(size(irow,1));

% Use f11za to get Compressed column storage array icolzp.
irow = int64(irow);
icol = int64(icol);
dup = 'S';
zero = 'K';
[nz, a, icol, irow, icolzp, ifail] = ...
  f11za(...
        n, nz, a, icol, irow, dup, zero);

% Perform bandwidth reduction
use_mask  = false;
do_cm     = false;
check_sym = true;
bw_before = true;
bw_after  = true;
lopts(1:5) = [use_mask,do_cm,check_sym,bw_before,bw_after];
mask       = [int64(0)];

[perm, info, ifail] = f11ye( ...
                             icolzp, irow, lopts, mask);

% Display results
disp('Permutation (perm):');
fprintf(' %4d %4d %4d %4d %4d %4d %4d %4d %4d %4d\n',perm)
fprintf('\nStatistics:\n');
fprintf('  Before:  Bandwidth = %6d\n', info(1));
fprintf('  Before:  Profile   = %6d\n', info(2));
fprintf('  After :  Bandwidth = %6d\n', info(3));
fprintf('  After :  Profile   = %6d\n', info(4));

% Permuted matrix
B = A(perm,perm);

fig1 = figure;
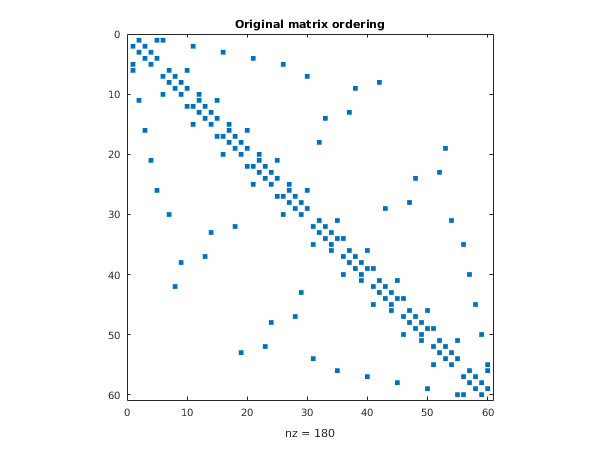
spy(A);
title('Original matrix ordering');
fig2 = figure;
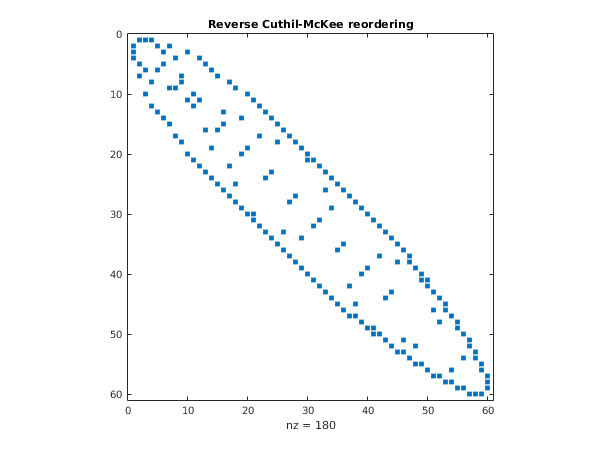
spy(B);
title('Reverse Cuthil-McKee reordering');

f11ye example results

Permutation (perm):
    1    5    2    6    4    3   26    7   30   11
   12   10   21   16   27   25    8   29   17   15
   13    9   22   20   28   24   42   43   18   14
   37   38   23   19   47   48   41   44   32   33
   36   39   52   53   46   49   45   31   34   40
   51   54   50   58   35   57   55   59   56   60

Statistics:
  Before:  Bandwidth =     34
  Before:  Profile   =    490
  After :  Bandwidth =     10
  After :  Profile   =    458