NAG Toolbox: nag_eigen_real_gen_sparse_arnoldi (f02ek)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{n}$ – int64int32nag_int scalar

$n$, the order of the matrix $A$.

Constraint: $\mathbf{n}\ge 0$.

2:     $\mathrm{a}\left(\mathbf{nz}\right)$ – double array

The array of nonzero elements (and diagonal elements if a nonzero inverse shift is to be applied) of the $n$ by $n$ general matrix $A$.

3:     $\mathrm{icolzp}\left(\mathbf{n}+1\right)$ – int64int32nag_int array

$\mathbf{icolzp}\left(i\right)$ contains the index in a of the start of column $\mathit{i}$, for $\mathit{i}=1,2,\dots ,n$; $\mathbf{icolzp}\left(\mathbf{n}+1\right)$ must contain the value $\mathbf{nz}+1$. Thus the number of nonzero elements in column $\mathit{i}$ of $A$ is $\mathbf{icolzp}\left(i+1\right)-\mathbf{icolzp}\left(i\right)$; when shifts are applied this includes diagonal elements irrespective of value. See Compressed column storage (CCS) format in the F11 Chapter Introduction.

4:     $\mathrm{irowix}\left(\mathbf{nz}\right)$ – int64int32nag_int array

$\mathbf{irowix}\left(i\right)$ contains the row index for each entry in a. See Compressed column storage (CCS) format in the F11 Chapter Introduction.

5:     $\mathrm{nev}$ – int64int32nag_int scalar

The number of eigenvalues to be computed.

Constraint: $0<\mathbf{nev}<\mathbf{n}-1$.

6:     $\mathrm{ncv}$ – int64int32nag_int scalar

The dimension of the array w. the number of Arnoldi basis vectors to use during the computation.

At present there is no a priori analysis to guide the selection of ncv relative to nev. However, it is recommended that $\mathbf{ncv}\ge 2\times \mathbf{nev}+1$. If many problems of the same type are to be solved, you should experiment with increasing ncv while keeping nev fixed for a given test problem. This will usually decrease the required number of matrix-vector operations but it also increases the work and storage required to maintain the orthogonal basis vectors. The optimal ‘cross-over’ with respect to CPU time is problem dependent and must be determined empirically.

Constraint: $\mathbf{nev}+1<\mathbf{ncv}\le \mathbf{n}$.

7:     $\mathrm{sigma}$ – double scalar

If the Shifted Inverse Real mode has been selected then sigma contains the real shift used; otherwise sigma is not referenced. This mode can be selected by setting the appropriate options in the user-supplied function option.

8:     $\mathrm{monit}$ – function handle or string containing name of m-file

monit is used to monitor the progress of nag_eigen_real_gen_sparse_arnoldi (f02ek). monit may be the dummy function nag_eigen_arnoldi_monit_gen (f02ekz) if no monitoring is actually required. (nag_eigen_arnoldi_monit_gen (f02ekz) is included in the NAG Toolbox.) monit is called after the solution of each eigenvalue sub-problem and also just prior to return from nag_eigen_real_gen_sparse_arnoldi (f02ek).

[istat, user] = monit(ncv, niter, nconv, w, rzest, istat, user)

Input Parameters

1:     $\mathrm{ncv}$ – int64int32nag_int scalar

The dimension of the arrays w and rzest. The number of Arnoldi basis vectors used during the computation.

2:     $\mathrm{niter}$ – int64int32nag_int scalar

The number of the current Arnoldi iteration.

3:     $\mathrm{nconv}$ – int64int32nag_int scalar

The number of converged eigenvalues so far.

4:     $\mathrm{w}\left(\mathbf{ncv}\right)$ – complex array

The first nconv elements of w contain the converged approximate eigenvalues.

5:     $\mathrm{rzest}\left(\mathbf{ncv}\right)$ – double array

The first nconv elements of rzest contain the Ritz estimates (error bounds) on the converged approximate eigenvalues.

6:     $\mathrm{istat}$ – int64int32nag_int scalar

Set to zero.

7:     $\mathrm{user}$ – Any MATLAB object

monit is called from nag_eigen_real_gen_sparse_arnoldi (f02ek) with the object supplied to nag_eigen_real_gen_sparse_arnoldi (f02ek).

Output Parameters

1:     $\mathrm{istat}$ – int64int32nag_int scalar

If set to a nonzero value nag_eigen_real_gen_sparse_arnoldi (f02ek) returns immediately with $\mathbf{ifail}=\mathbf{9}$.

2:     $\mathrm{user}$ – Any MATLAB object

9:     $\mathrm{option}$ – function handle or string containing name of m-file

You can supply non-default options to the Arnoldi eigensolver by repeated calls to nag_sparseig_real_option (f12ad) from within option. (Please note that it is only necessary to call nag_sparseig_real_option (f12ad); no call to nag_sparseig_real_init (f12aa) is required from within option.) For example, you can set the mode to Shifted Inverse Real, you can increase the Iteration Limit beyond its default and you can print varying levels of detail on the iterative process using Print Level.

If only the default options (including that the eigenvalues of largest magnitude are sought) are to be used then option may be the dummy function nag_eigen_arnoldi_option (f02eky) (nag_eigen_arnoldi_option (f02eky) is included in the NAG Toolbox). See Example for an example of using option to set some non-default options.

[icomm, comm, istat, user] = option(icomm, comm, istat, user)

Input Parameters

1:     $\mathrm{icomm}\left(:\right)$ – int64int32nag_int array

Contains details of the default option set. This array must be passed as argument icomm in any call to nag_sparseig_real_option (f12ad).

2:     $\mathrm{comm}\left(:\right)$ – double array

Contains details of the default option set. This array must be passed as argument comm in any call to nag_sparseig_real_option (f12ad).

3:     $\mathrm{istat}$ – int64int32nag_int scalar

Set to zero.

4:     $\mathrm{user}$ – Any MATLAB object

option is called from nag_eigen_real_gen_sparse_arnoldi (f02ek) with the object supplied to nag_eigen_real_gen_sparse_arnoldi (f02ek).

Output Parameters

1:     $\mathrm{icomm}\left(:\right)$ – int64int32nag_int array

Contains data on the current options set which may be altered from the default set via calls to nag_sparseig_real_option (f12ad).

2:     $\mathrm{comm}\left(:\right)$ – double array

Contains data on the current options set which may be altered from the default set via calls to nag_sparseig_real_option (f12ad).

3:     $\mathrm{istat}$ – int64int32nag_int scalar

If set to a nonzero value nag_eigen_real_gen_sparse_arnoldi (f02ek) returns immediately with $\mathbf{ifail}=\mathbf{10}$.

4:     $\mathrm{user}$ – Any MATLAB object

Optional Input Parameters

1:     $\mathrm{nz}$ – int64int32nag_int scalar

Default: the dimension of the array a and the dimension of the array irowix. (An error is raised if these dimensions are not equal.)

The dimension of the array a and the number of nonzero elements of the matrix $A$ and, if a nonzero shifted inverse is to be applied, all diagonal elements. Each nonzero is counted once in the latter case.

Constraint: $0\le \mathbf{nz}\le {\mathbf{n}}^2$.

2:     $\mathrm{user}$ – Any MATLAB object

user is not used by nag_eigen_real_gen_sparse_arnoldi (f02ek), but is passed to monit and option. Note that for large objects it may be more efficient to use a global variable which is accessible from the m-files than to use user.

Output Parameters

1:     $\mathrm{a}\left(\mathbf{nz}\right)$ – double array

If a nonzero shifted inverse is to be applied then the diagonal elements of $A$ have the shift value, as supplied in sigma, subtracted.

2:     $\mathrm{nconv}$ – int64int32nag_int scalar

The number of converged approximations to the selected eigenvalues. On successful exit, this will normally be either nev or $\mathbf{nev}+1$ depending on the number of complex conjugate pairs of eigenvalues returned.

3:     $\mathrm{w}\left(\mathbf{ncv}\right)$ – complex array

The first nconv elements contain the converged approximations to the selected eigenvalues. Since complex conjugate pairs of eigenvalues appear together, it is possible (given an odd number of converged real eigenvalues) for nag_eigen_real_gen_sparse_arnoldi (f02ek) to return one more eigenvalue than requested.

4:     $\mathrm{v}\left(\mathit{ldv},:\right)$ – double array

The first dimension of the array v will be $\mathbf{n}$.

The second dimension of the array v will be $\mathbf{ncv}$.

Contains the eigenvectors associated with the eigenvalue ${\lambda }_{\mathit{i}}$, for $\mathit{i}=1,2,\dots ,\mathbf{nconv}$ (stored in w). For a real eigenvalue, ${\lambda }_j$, the corresponding eigenvector is real and is stored in $\mathbf{v}\left(\mathit{i},j\right)$, for $\mathit{i}=1,2,\dots ,n$. For complex conjugate pairs of eigenvalues, $w_{j+1}=\stackrel{-}{w_j}$, the real and imaginary parts of the corresponding eigenvectors are stored, respectively, in $\mathbf{v}\left(\mathit{i},j\right)$ and $\mathbf{v}\left(\mathit{i},j\right)$, for $\mathit{i}=1,2,\dots ,n$. The imaginary parts stored are for the first of the conjugate pair of eigenvectors; the other eigenvector in the pair is obtained by negating these imaginary parts.

5:     $\mathrm{resid}\left(\mathbf{nev}+1\right)$ – double array

The residual ${‖A{w}_{\mathit{i}}-{\lambda }_{\mathit{i}}{w}_{\mathit{i}}‖}_2$ for the estimates to the eigenpair ${\lambda }_{\mathit{i}}$ and $w_{\mathit{i}}$ is returned in $\mathbf{resid}\left(\mathit{i}\right)$, for $\mathit{i}=1,2,\dots ,\mathbf{nconv}$.

6:     $\mathrm{user}$ – Any MATLAB object

7:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

   $\mathbf{ifail}=1$

Constraint: $\mathbf{n}>0$.

   $\mathbf{ifail}=2$

Constraint: $\mathbf{nz}>0$.

Constraint: $\mathbf{nz}\le \mathbf{n}\times \mathbf{n}$.

   $\mathbf{ifail}=3$

On entry, in shifted inverse mode, the $j$th diagonal element of $A$ is not defined.

   $\mathbf{ifail}=4$

Constraint: $\mathbf{icolzp}\left(1\right)=1$.

Constraint: $\mathbf{icolzp}\left(i\right)<\mathbf{icolzp}\left(i+1\right)$.

Constraint: $\mathbf{icolzp}\left(\mathbf{n}+1\right)=\mathbf{nz}+1$.

   $\mathbf{ifail}=5$

Constraint: $\mathbf{irowix}\left(j\right)<\mathbf{irowix}\left(j+1\right)$.

   $\mathbf{ifail}=6$

Constraint: $\mathbf{nev}>0$.

   $\mathbf{ifail}=7$

Constraint: $\mathbf{ncv}>\mathbf{nev}+1$.

Constraint: $\mathbf{ncv}\le \mathbf{n}$.

   $\mathbf{ifail}=8$

On entry, the matrix $A-\sigma \times I$ is nearly numerically singular and could not be inverted.

On entry, the matrix $A-\sigma \times I$ is numerically singular and could not be inverted. Try perturbing the value of $\sigma$.

   $\mathbf{ifail}=9$

User requested termination in monit.

   $\mathbf{ifail}=10$

User requested termination in option.

   $\mathbf{ifail}=14$

Constraint: $\mathit{ldv}\ge \mathbf{n}$.

   $\mathbf{ifail}=21$

The maximum number of iterations $\le 0$, the optional parameter Iteration Limit has been set.

   $\mathbf{ifail}=22$

An internal call to nag_sparseig_real_iter (f12ab) returned with $\mathbf{ifail}=\mathbf{2}$.
This error should not occur. Please contact NAG.

   $\mathbf{ifail}=23$

An internal call to nag_sparseig_real_iter (f12ab) returned with $\mathbf{ifail}=\mathbf{3}$.

   $\mathbf{ifail}=24$

The maximum number of iterations has been reached.

   $\mathbf{ifail}=25$

No shifts could be applied during a cycle of the implicitly restarted Arnoldi iteration.

   $\mathbf{ifail}=26$

Could not build an Arnoldi factorization.

   $\mathbf{ifail}=27$

Error in internal call to compute eigenvalues and corresponding error bounds of the current upper Hessenberg matrix.
Please contact NAG.

   $\mathbf{ifail}=32$

An internal call to nag_sparseig_real_proc (f12ac) returned with $\mathbf{ifail}=\mathbf{2}$.

   $\mathbf{ifail}=33$

The number of eigenvalues found to sufficient accuracy is zero.

   $\mathbf{ifail}=34$

Internal inconsistency in the number of converged Ritz values.

   $\mathbf{ifail}=35$

During calculation of a real Schur form, there was a failure to compute $\_$ eigenvalues in a total of $\_$ iterations.

   $\mathbf{ifail}=36$

The computed Schur form could not be reordered by an internal call.

   $\mathbf{ifail}=37$

In calculating eigenvectors, an internal call returned with an error.
Please contact NAG.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Example

Open in the MATLAB editor: f02ek_example

function f02ek_example


fprintf('f02ek example results\n\n');


% This example demonstrates the use of f02ek to evaluate a number of
% eigenvalues of a sparse matrix closest to a given value.

% Use existing sparse matrix.
load('west0479.mat')
W = west0479;

[irow,icol,a] = find(W);
n = int64(size(W,1));
nnz = int64(size(irow,1));

% Add zero diagonals to be summed
irow(nnz+1:nnz+n) = (1:n);
icol(nnz+1:nnz+n) = (1:n);
a(nnz+1:nnz+n) = 0.0;
nnz = nnz + n;

% Use f11za to get Compressed column storage array icolzp.
irow = int64(irow);
icol = int64(icol);
dup = 'S';
zero = 'K';
[nnz, a, icol, irow, icolzp, ifail] = ...
  f11za(...
        n, nnz, a, icol, irow, dup, zero);

% Evaluate nev eigenvalues (w) closest to sigma.
nev = int64(20);
ncv = int64(60);
sigma = 4.0;
% Set some options via user array and function argument option.
% user(1) = print level, iuser(2) = iteration limit,
% user(3)>0 means shifted-invert mode
% user(4)>0 means print monitoring info
user = [0, 500, 1, 0];

[a, nconv, w, v, resid, user, ifail] = ...
  f02ek(...
        n, a, icolzp, irow, nev, ncv, sigma, @monit, @option, 'user', user);

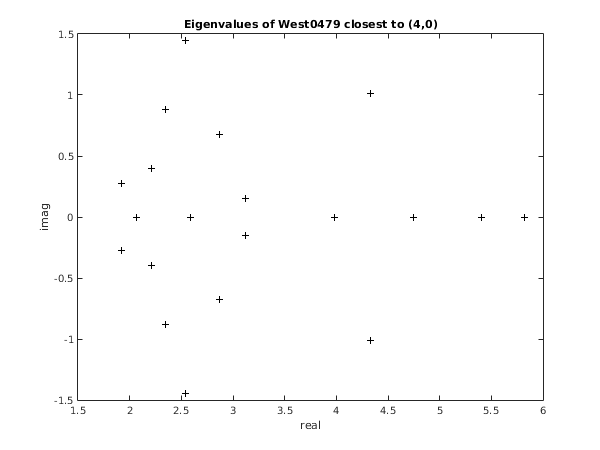
fprintf('\n The %d Ritz values closest to %8.2e are:\n', nconv, sigma);
disp(w(1:nconv));

fig1 = figure;
plot(w(1:nconv),'k+');
title('Eigenvalues of West0479 closest to (4,0)');
xlabel('real');
ylabel('imag');


function [istat, user] = monit(ncv, niter, nconv, w, rzest, istat, user);
  if (user(4)>0)
    if (niter==1 && user(3)>0)
      fprintf('The following Ritz values (mu) are related to the\n');
      fprintf('true eigenvalues (lambda) by lambda = sigma + 1/mu\n\n');
    end
    fprintf('Iteration number %d\n', niter);
    fprintf(' Ritz values converged so far (%d):\n', nconv);
    for i = 1:nconv
      fprintf(' %4d (%13.5e,%13.5e)\n',  i, real(w(i)), imag(w(i)));
    end
    fprintf(' Next (unconverged) Ritz value:\n');
    fprintf(' %4d (%13.5e,%13.5e)\n', nconv+1, real(w(nconv+1)), ...
            imag(w(nconv+1)));
  end
  istat = int64(0);

function [icomm, comm, istat, user] = option(icomm, comm, istat, user);
  if (user(1)>0)
    [icomm, comm, ifail] = ...
      f12ad(strcat('Print Level=', int2str(user(1))), icomm, comm);
    istat = max(istat,ifail);
  end
  if (user(2)>100)
    [icomm, comm, ifail] = ...
      f12ad(strcat('Iteration Limit=', int2str(user(2))), icomm, comm);
    istat = max(istat,ifail);
  end
  if (user(3)>0)
    [icomm, comm, ifail] = ...
      f12ad('Shifted Inverse Real', icomm, comm);
    istat = max(istat,ifail);
  end

f02ek example results


 The 20 Ritz values closest to 4.00e+00 are:
   3.9852 + 0.0000i
   4.7459 + 0.0000i
   3.1237 - 0.1509i
   3.1237 + 0.1509i
   4.3290 - 1.0151i
   4.3290 + 1.0151i
   2.8651 - 0.6759i
   2.8651 + 0.6759i
   2.5930 + 0.0000i
   5.4060 + 0.0000i
   5.8229 + 0.0000i
   2.3494 - 0.8839i
   2.3494 + 0.8839i
   2.2071 - 0.3953i
   2.2071 + 0.3953i
   2.5364 - 1.4458i
   2.5364 + 1.4458i
   2.0675 + 0.0000i
   1.9248 - 0.2785i
   1.9248 + 0.2785i

Optional Parameters

• Advisory
• Defaults
• Iteration Limit
• Largest Imaginary
• Largest Magnitude
• Largest Real
• List
• Monitoring
• Nolist
• Print Level
• Regular
• Shifted Inverse Real
• Smallest Imaginary
• Smallest Magnitude
• Smallest Real
• Tolerance

Description of the Optional Parameters

• the keywords, where the minimum abbreviation of each keyword is underlined;
• a parameter value, where the letters $a$, $i$ and $r$ denote options that take character, integer and real values respectively;
• the default value, where the symbol $\epsilon$ is a generic notation for machine precision (see nag_machine_precision (x02aj)).