Open in the MATLAB editor: e02jf_example
function e02jf_example fprintf('e02jf example results\n\n'); xdata = [0; 0.5; 1; 1.5; 2; 2.5; 3; 4; 4.5; 5; 5.5; 6; 7; 7.5; 8]; ydata = [-1.1; -0.372; 0.431; 1.69; 2.11; 3.1; 4.23; 4.35; 4.81; 4.61; 4.79; ... 5.23; 6.35; 7.19; 7.97]; wdata = [1; 1; 1.5; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1]; cstart = 'c'; sfac = 0.001; x = [6.5178; 7.2463; 1.0159; 7.3070; 5.0589; 0.7803; 2.2280; 4.3751; ... 7.6601; 7.7191; 1.2609; 7.7647; 7.6573; 3.8830; 6.4022; 1.1351; ... 3.3741; 7.3259; 6.3377; 7.6759]; nest = int64(numel(xdata) + 4); ixloc = zeros(numel(x), 1, 'int64'); wrk = zeros(4*numel(xdata) + 16*nest + 41, 1); iwrk1 = zeros(nest, 1, 'int64'); iwrk2 = zeros(3+3*numel(x), 1, 'int64'); lamda = zeros(nest, 1); xord = int64(0); start = int64(0); deriv = int64(3); % Generate the data to fit. [x, y, f, lsminp, lsmaxp, nxcels, nycels] = generate_data(); % Initialize the options arrays and set/get some options. [iopts, opts] = handle_options(); % Compute the spline coefficients. [coefs, iopts, opts, ifail] = ... e02jd(x, y, f, lsminp, lsmaxp, nxcels, nycels, iopts, opts); % pmin and pmax form the bounding box of the spline. We must not attempt to % evaluate the spline outside this box. pmin = [min(x); min(y)]; pmax = [max(x); max(y)]; % Evaluate the approximation at a vector of values. evaluate_at_vector(coefs, iopts, opts, pmin, pmax); % Evaluate the approximation on a mesh. evaluate_on_mesh(coefs, iopts, opts, pmin, pmax); function [x, y, f, lsminp, lsmaxp, nxcels, nycels] = generate_data() % Generates an x and a y vector of n pseudorandom uniformly distributed % values on (0,1]. These are passed to the bivariate function of R. Franke % to create the data set to fit. The remaining input data for % e02jd are set to suitable values for this problem, % as discussed by Davydov and Zeilfelder. n = int64(100); % Initialize the generator to a repeatable sequence [state, ifail] = g05kf(int64(1), int64(0), int64(32958)); % Generate x values [state, x, ifail] = g05sa(n, state); % Generate y values [state, y, ifail] = g05sa(n, state); % Ensure that the bounding box stretches all the way to (0,0) and (1,1) x(1) = 0; y(1) = 0; x(n) = 1; y(n) = 1; f = 0.75*exp(-((9*x(:)-2).^2 + (9*y(:)-2).^2)/4) + ... 0.75*exp(-((9*x(:)+1).^2/49 + (9*y(:)+1)/10)) + ... 0.50*exp(-((9*x(:)-7).^2 + (9*y(:)-3).^2)/4) - ... 0.20*exp(-((9*x(:)-4).^2 + (9*y(:)-7).^2)); % Grid size for the approximation nxcels = int64(6); nycels = int64(6); % Identify the computation. fprintf(['\nComputing the coefficients of a C^1 spline',... ' approximation to Franke''s function\n']); fprintf(' Using a %d by %d grid\n', nxcels, nycels); % Local-approximation control parameters. lsminp = int64(3); lsmaxp = int64(100); function [iopts, opts] = handle_options() % Initialize the options arrays and demonstrate how to set and get % optional parameters. opts = zeros(100, 1); iopts = zeros(100, 1, 'int64'); [iopts, opts, ifail] = e02zk( ... 'Initialize = e02jd', iopts, opts); % Set some non-default parameters for the local approximation method. optstr = strcat('Minimum Singular Value LPA = ', num2str(1/32)); [iopts, opts, ifail] = e02zk( ... optstr, iopts, opts); [iopts, opts, ifail] = e02zk( ... 'Polynomial Starting Degree = 3', iopts, opts); % Set a non-default parameter for the global approximation method. [iopts, opts, ifail] = e02zk( ... 'Averaged Spline = Yes', iopts, opts); % As an example of how to get the value of an optional parameter, % display whether averaging of local approximations is in operation. [~, ~, cvalue, ~, ifail] = e02zl( ... 'Averaged Spline', iopts, opts); if strcmp(cvalue, 'YES') fprintf(' Using an averaged local approximation\n'); end function evaluate_at_vector(coefs, iopts, opts, pmin, pmax) % Evaluates the approximation at a (in this case trivial) vector of values. xevalv = [0]; yevalv = [0]; % Force the points to be within the bounding box of the spline for i = 1:numel(xevalv) xevalv(i) = max(xevalv(i),pmin(1)); xevalv(i) = min(xevalv(i),pmax(1)); yevalv(i) = max(yevalv(i),pmin(2)); yevalv(i) = min(yevalv(i),pmax(2)); end [fevalv, ifail] = e02je(xevalv, yevalv, coefs, iopts, opts); fprintf('\n Values of computed spline at (x_i,y_i):\n\n'); fprintf(' x_i y_i f(x_i,y_i)\n'); for i = 1:numel(xevalv) fprintf('%12.2f %12.2f %12.2f\n', xevalv(i),yevalv(i),fevalv(i)); end function evaluate_on_mesh(coefs,iopts,opts,pmin,pmax) % Evaluates the approximation on a mesh of n_x * n_y values. nxeval = 101; nyeval = 101; % Define the mesh by its lower-left and upper-right corners. ll_corner = [0; 0]; ur_corner = [1; 1]; % Set the mesh spacing and the evaluation points. % Force the points to be within the bounding box of the spline. h = [(ur_corner(1)-ll_corner(1))/(nxeval-1); ... (ur_corner(2)-ll_corner(2))/(nyeval-1)]; xevalm = ll_corner(1) + [0:nxeval-1]*h(1); yevalm = ll_corner(2) + [0:nyeval-1]*h(2); % Ensure that the evaluation points are in the bounding box xevalm = max(pmin(1), xevalm); xevalm = min(pmax(1), xevalm); yevalm = max(pmin(2), yevalm); yevalm = min(pmax(2), yevalm); % Evaluate [fevalm, ifail] = e02jf(xevalm, yevalm, coefs, iopts, opts); print_mesh = false; if print_mesh fprintf('\nValues of computed spline at (x_i,y_j):\n\n'); fprintf(' x_i y_i f(x_i,y_i)\n'); for i = 1:nxeval for j=1:nyeval fprintf('%12.2f %12.2f %12.2f\n', xevalm(i),yevalm(j),fevalm(i, j)); end end else fprintf('\nOutputting of the function values on the mesh is disabled\n'); end fig1 = figure; meshc(yevalm,xevalm,fevalm); title({'Bivariate spline fit from scattered data', ... 'using two-stage approximation'}); xlabel('x'); ylabel('y'); view(22,28);
e02jf example results
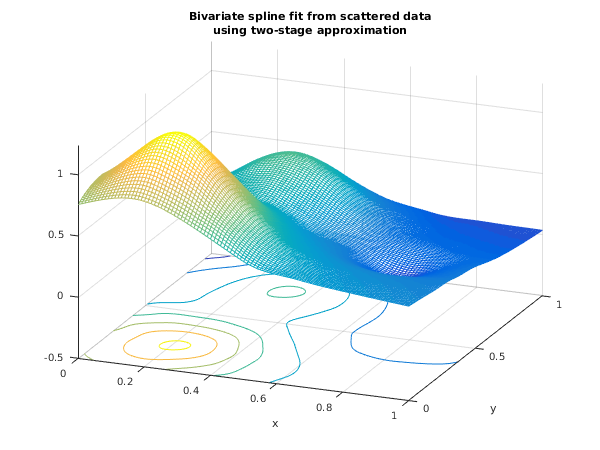
Computing the coefficients of a C^1 spline approximation to Franke's function
Using a 6 by 6 grid
Using an averaged local approximation
Values of computed spline at (x_i,y_i):
x_i y_i f(x_i,y_i)
0.00 0.00 0.76
Outputting of the function values on the mesh is disabled
