PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_mesh_2d_gen_boundary (d06ba)
Purpose
nag_mesh_2d_gen_boundary (d06ba) generates a boundary mesh on a closed connected subdomain of .
Syntax
[
nvb,
coor,
nedge,
edge,
user,
ifail] = d06ba(
coorch,
lined,
fbnd,
crus,
rate,
nlcomp,
lcomp,
nvmax,
nedmx,
itrace, 'nlines',
nlines, 'sdcrus',
sdcrus, 'ncomp',
ncomp, 'user',
user)
[
nvb,
coor,
nedge,
edge,
user,
ifail] = nag_mesh_2d_gen_boundary(
coorch,
lined,
fbnd,
crus,
rate,
nlcomp,
lcomp,
nvmax,
nedmx,
itrace, 'nlines',
nlines, 'sdcrus',
sdcrus, 'ncomp',
ncomp, 'user',
user)
Description
Given a closed connected subdomain of , whose boundary is divided by characteristic points into distinct line segments, nag_mesh_2d_gen_boundary (d06ba) generates a boundary mesh on . Each line segment may be a straight line, a curve defined by the equation , or a polygonal curve defined by a set of given boundary mesh points.
This function is primarily designed for use with either
nag_mesh_2d_gen_inc (d06aa) (a simple incremental method) or
nag_mesh_2d_gen_delaunay (d06ab) (Delaunay–Voronoi method) or
nag_mesh_2d_gen_front (d06ac) (Advancing Front method) to triangulate the interior of the domain
. For more details about the boundary and interior mesh generation, consult the
D06 Chapter Introduction as well as
George and Borouchaki (1998).
This function is derived from material in the MODULEF package from INRIA (Institut National de Recherche en Informatique et Automatique).
References
George P L and Borouchaki H (1998) Delaunay Triangulation and Meshing: Application to Finite Elements Editions HERMES, Paris
Parameters
Compulsory Input Parameters
- 1:
– double array
-
contains the coordinate of the th characteristic point, for ; while contains the corresponding coordinate.
- 2:
– int64int32nag_int array
-
The description of the lines that define the boundary domain. The line
, for
, is defined as follows:
- The number of points on the line, including two end points.
- The first end point of the line. If , then the coordinates of the first end point are those stored in .
- The second end point of the line. If , then the coordinates of the second end point are those stored in .
- This defines the type of line segment connecting the end points. Additional information is conveyed by the numerical value of as follows:
| (i) |
, the line is described in fbnd with as the index. In this case, the line must be described in the trigonometric (anticlockwise) direction; |
| (ii) |
, the line is a straight line; |
| (iii) |
if , say (), then the line is a polygonal arc joining the end points and interior points specified in crus. In this case the line contains the points whose coordinates are stored in
,
where ,
,
and
. |
Constraints:
- ;
- ;
- ;
- , for .
For each line described by
fbnd (lines with
, for
) the two end points (
and
) lie on the curve defined by index
in
fbnd, i.e.,
;
, for .
For all lines described as polygonal arcs (lines with
, for
) the sets of intermediate points (i.e.,
for all
such that
) are not overlapping. This can be expressed as:
or
for a
such that
,
and
.
- 3:
– function handle or string containing name of m-file
-
fbnd must be supplied to calculate the value of the function which describes the curve
on segments of the boundary for which
.
If there are no boundaries for which
fbnd will never be referenced by
nag_mesh_2d_gen_boundary (d06ba) and
fbnd may be the string
'd06bad'. (
nag_mesh_2d_gen_boundary_dummy_fbnd (d06bad) is included in the NAG Toolbox.)
[result, user] = fbnd(ii, x, y, user)
Input Parameters
- 1:
– int64int32nag_int scalar
-
, the reference index of the line (portion of the contour) described.
- 2:
– double scalar
- 3:
– double scalar
-
The values of and at which is to be evaluated.
- 4:
– Any MATLAB object
fbnd is called from
nag_mesh_2d_gen_boundary (d06ba) with the object supplied to
nag_mesh_2d_gen_boundary (d06ba).
Output Parameters
- 1:
– double scalar
-
The value of at the specified point.
- 2:
– Any MATLAB object
- 4:
– double array
-
The coordinates of the intermediate points for polygonal arc lines. For a line defined as a polygonal arc (i.e., ), if , then
, for , must contain the coordinate of the consecutive intermediate points for this line. Similarly
, for , must contain the corresponding coordinate.
- 5:
– double array
-
is the geometric progression ratio between the points to be generated on the line
, for
and
.
If , is not referenced.
Constraint:
if , , for .
- 6:
– int64int32nag_int array
-
is the number of line segments in component of the contour. The line of component runs in the direction to if , and in the opposite direction otherwise; for .
Constraints:
- , for ;
- .
- 7:
– int64int32nag_int array
-
lcomp must contain the list of line numbers for the each component of the boundary. Specifically, the line numbers for the
th component of the boundary, for
, must be in elements
to
of
lcomp, where
and
.
Constraint:
must hold a valid permutation of the integers .
- 8:
– int64int32nag_int scalar
-
The maximum number of the boundary mesh vertices to be generated.
Constraint:
.
- 9:
– int64int32nag_int scalar
-
The maximum number of boundary edges in the boundary mesh to be generated.
Constraint:
.
- 10:
– int64int32nag_int scalar
-
The level of trace information required from
nag_mesh_2d_gen_boundary (d06ba).
- or
- No output is generated.
- Output from the boundary mesh generator is printed on the current advisory message unit (see nag_file_set_unit_advisory (x04ab)). This output contains the input information of each line and each connected component of the boundary.
- An analysis of the output boundary mesh is printed on the current advisory message unit. This analysis includes the orientation (clockwise or anticlockwise) of each connected component of the boundary. This information could be of interest to you, especially if an interior meshing is carried out using the output of this function, calling either nag_mesh_2d_gen_inc (d06aa), nag_mesh_2d_gen_delaunay (d06ab) or nag_mesh_2d_gen_front (d06ac).
- The output is similar to that produced when , but the coordinates of the generated vertices on the boundary are also output.
You are advised to set , unless you are experienced with finite element mesh generation.
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the arrays
coorch,
lined,
rate,
lcomp. (An error is raised if these dimensions are not equal.)
, the number of lines that define the boundary of the closed connected subdomain (this equals the number of characteristic points which separate the entire boundary into lines).
Constraint:
.
- 2:
– int64int32nag_int scalar
-
Default:
the second dimension of the array
crus.
The second dimension of the array
crus.
Constraint:
.
- 3:
– int64int32nag_int scalar
-
Default:
the dimension of the array
nlcomp.
, the number of separately connected components of the boundary.
Constraint:
.
- 4:
– Any MATLAB object
user is not used by
nag_mesh_2d_gen_boundary (d06ba), but is passed to
fbnd. Note that for large objects it may be more efficient to use a global variable which is accessible from the m-files than to use
user.
Output Parameters
- 1:
– int64int32nag_int scalar
-
The total number of boundary mesh vertices generated.
- 2:
– double array
-
will contain the coordinate of the th boundary mesh vertex generated, for ; while will contain the corresponding coordinate.
- 3:
– int64int32nag_int scalar
-
The total number of boundary edges in the boundary mesh.
- 4:
– int64int32nag_int array
-
The specification of the boundary edges.
and
will contain the vertex numbers of the two end points of the
th boundary edge.
is a reference number for the
th boundary edge and
- , where and are such that the th edges is part of the th line of the boundary and ;
- , where and are such that the th edges is part of the th line of the boundary and .
- 5:
– Any MATLAB object
- 6:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
| On entry, | ; |
| or | ; |
| or | ; |
| or | ; |
| or | ; |
| or | ; |
| or | ; |
| or | for some with ; |
| or | for some ; |
| or | or for some ; |
| or | or for some ; |
| or | for some ; |
| or | , or for a ; |
| or | ; |
| or | lcomp does not represent a valid permutation of the integers in ; |
| or | one of the end points for a line described by the user-supplied function (lines with
, for ) does not belong to the corresponding curve in fbnd; |
| or | the intermediate points for the lines described as polygonal arcs (lines with , for ) are overlapping. |
-
-
An error has occurred during the generation of the boundary mesh. It appears that
nedmx is not large enough, so you are advised to increase the value of
nedmx.
-
-
An error has occurred during the generation of the boundary mesh. It appears that
nvmax is not large enough, so you are advised to increase the value of
nvmax.
-
-
An error has occurred during the generation of the boundary mesh. Check the definition of each line (the argument
lined) and each connected component of the boundary (the arguments
nlcomp, and
lcomp, as well as the coordinates of the characteristic points. Setting
may provide more details.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
Not applicable.
Further Comments
The boundary mesh generation technique in this function has a ‘tree’ structure. The boundary should be partitioned into geometrically simple segments (straight lines or curves) delimited by characteristic points. Then, the lines should be assembled into connected components of the boundary domain.
Using this strategy, the inputs to that function can be built up, following the requirements stated in
Arguments:
- the characteristic and the user-supplied intermediate points:
- the characteristic lines:
- finally the assembly of lines into the connected components of the boundary:
The example below details the use of this strategy.
Example
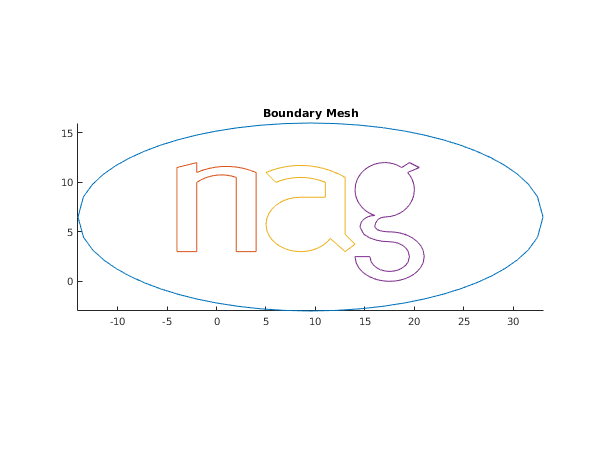
The NAG logo is taken as an example of a geometry with holes. The boundary has been partitioned in
lines characteristic points; including
for the exterior boundary and
for the logo itself. All line geometry specifications have been considered, see the description of
lined, including
lines defined as polygonal arc,
defined by
fbnd and all the others are straight lines.
Open in the MATLAB editor:
d06ba_example
function d06ba_example
fprintf('d06ba example results\n\n');
nlines = 45;
line = zeros(4,nlines,'int64');
line(1:4,1:nlines) = [ 15 1 2 1; 15 2 3 1; 15 3 4 1;
15 4 1 1; 4 6 5 -1; 10 10 6 0;
10 14 10 2; 10 7 14 0; 4 8 7 0;
10 13 8 0; 10 13 9 3; 10 12 9 0;
4 11 12 0; 15 5 11 0; 15 26 15 4;
10 26 25 0; 4 25 24 0; 4 24 23 0;
4 23 22 0; 10 21 22 6; 10 20 21 6;
10 19 20 6; 4 19 18 0; 5 18 17 0;
15 17 16 5; 4 16 15 0; 4 27 28 0;
7 28 30 8; 7 30 32 8; 7 32 34 8;
6 36 34 10; 6 38 36 12; 10 40 38 13;
10 42 40 13; 8 44 42 13; 4 44 45 0;
4 45 43 0; 4 43 41 0; 6 39 41 13;
10 37 39 13; 6 37 35 11; 6 35 33 9;
10 31 33 7; 10 29 31 7; 10 27 29 7]';
coorch = zeros(2,nlines);
coorch(1,:) = ...
[ 9.5 33.0 9.5 -14.0 ...
-4.0 -2.0 2.0 4.0 -2.0 -2.0 -4.0 -2.0 4.0 2.0 ...
5.0 6.0 11.0 11.0 8.5 5.0 8.5 11.5 13.0 14.0 13.0 13.0 ...
14.0 15.5 17.5 17.5 21.0 19.5 17.5 17.5 16.0 14.5 ...
17.0 16.0 20.0 14.0 19.3142 17.0 20.5 18.7249 19.5];
coorch(2,:) = ...
[-3.0 6.5 16.0 6.5 ...
3.0 3.0 3.0 3.0 11.0 10.0 11.5 12.0 11.0 10.5 ...
11.0 10.0 10.0 8.5 8.5 5.75 3.0 4.3335 3.0 3.75 4.75 10.5 ...
2.5 2.5 0.0 1.0 2.5 2.5 5.0 4.0 5.5 5.5 ...
6.5 6.6573 9.25 9.25 11.0 12.0 11.5 11.5 12.0];
crus = zeros(2, 2);
crus(1,1:2)=[-8,-10]/3;
crus(2,1:2) = [3,3];
rate = ones(nlines,1);
rate(1:4,1) = [0.95;1.05;0.95;1.05];
nlcomp = int64([4 10 12 19]);
lcomp = zeros(nlines,1,'int64');
lcomp(1:nlines,1) = [ 1 2 3 4 ...
14 13 12 11 10 9 8 7 6 5 ...
18 19 20 21 22 23 24 25 26 15 16 17 ...
27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45];
nvmax = int64(5000);
nedmx = int64(1000);
itrace = int64(-1);
user = [23.5; 9.5; 9.5; 6.5];
[nvb, coor, nedge, edge, user, ifail] = ...
d06ba( ...
coorch, line, @fbnd, crus, rate, nlcomp, lcomp, nvmax, ...
nedmx, itrace, 'user', user);
i = int64(0);
k = int64(0);
fig1 = figure;
hold on;
title('Boundary Mesh');
for seg = 1:4
i0 = i;
for j = k+1:k+nlcomp(seg)
i = i + line(1,lcomp(j,1));
end
k = k + nlcomp(seg);
i = i - nlcomp(seg);
segl = i - i0;
for j = 1:segl
segx(j) = coor(1,i0+j);
segy(j) = coor(2,i0+j);
end
segx(segl+1) = segx(1);
segy(segl+1) = segy(1);
plot(segx(1:segl+1),segy(1:segl+1));
end
axis equal tight;
npropa = int64(1);
itrace = int64(0);
weight = [];
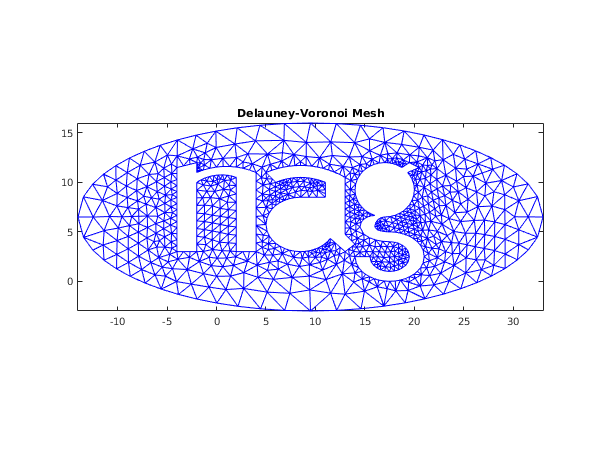
[nv, nelt, coor, conn, ifail] = ...
d06ab( ...
nvb, edge, coor, weight, npropa, itrace,'nedge',nedge);
fig2 = figure;
triplot(transpose(double(conn(:,1:nelt))), coor(1,:), coor(2,:));
title('Delauney-Voronoi Mesh');
axis equal tight;
fprintf('\nComplete mesh characteristics for Delauney-Voronoi mesh:\n');
fprintf('Number of vertices = %4d\n',nv);
fprintf('Number of elements = %4d\n',nelt);
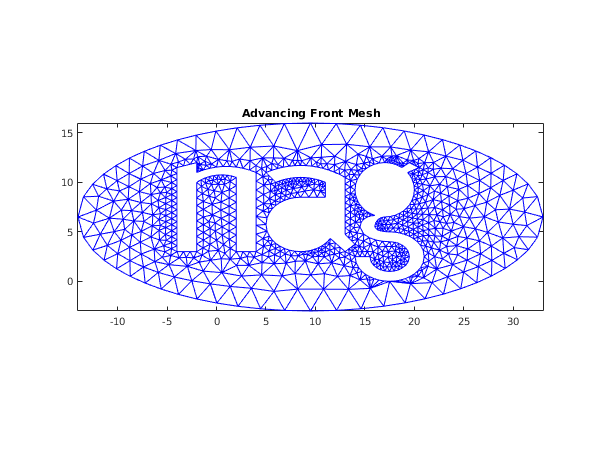
[nv, nelt, coor, conn, ifail] = ...
d06ac( ...
nvb, edge(:,1:nedge), coor, weight, itrace);
fig3 = figure;
triplot(transpose(double(conn(:,1:nelt))), coor(1,:), coor(2,:));
title('Advancing Front Mesh');
axis equal tight;
fprintf('\nComplete mesh characteristics for advancing front mesh:\n');
fprintf('Number of vertices = %4d\n',nv);
fprintf('Number of elements = %4d\n',nelt);
function [result, user] = fbnd(i, x, y, user)
xa = user(1);
xb = user(2);
x0 = user(3);
y0 = user(4);
result = 0;
if (i == 1)
result = ((x-x0)/xa)^2 + ((y-y0)/xb)^2 - 1;
elseif (i == 2)
x0 = 0.5;
y0 = 6.25;
radius2 = 20.3125;
result = (x-x0)^2 + (y-y0)^2 - radius2;
elseif (i == 3)
x0 = 1;
y0 = 4;
radius2 = 9 + (11-y0)^2;
result = (x-x0)^2 + (y-y0)^2 - radius2;
elseif (i == 4)
x0 = 8.5;
y0 = 2.75;
radius2 = (x0-5)^2 + (11-y0)^2;
result = (x-x0)^2 + (y-y0)^2 - radius2;
elseif (i == 5)
x0 = 8.5;
y0 = 4;
radius2 = 2.5^2 + (10-y0)^2;
result = (x-x0)^2 + (y-y0)^2 - radius2;
elseif (i == 6)
x0 = 8.5;
y0 = 5.75;
result = ((x-x0)/3.5)^2 + ((y-y0)/2.75)^2 - 1;
elseif (i == 7)
x0 = 17.5;
y0 = 2.5;
result = ((x-x0)/3.5)^2 + ((y-y0)/2.5)^2 - 1;
elseif (i == 8)
x0 = 17.5;
y0 = 2.5;
result = ((x-x0)/2)^2 + ((y-y0)/1.5)^2 - 1;
elseif (i == 9)
x0 = 17.5;
y0 = 5.5;
result = ((x-x0)/1.5)^2 + ((y-y0)/0.5)^2 - 1;
elseif (i == 10)
x0 = 17.5;
y0 = 5.5;
result = ((x-x0)/3)^2 + ((y-y0)/1.5)^2 - 1;
elseif (i == 11)
x0 = 17.0;
y0 = 5.5;
result = ((x-x0))^2 + ((y-y0))^2 - 1;
elseif (i == 12)
x0 = 16;
y0 = 5.5;
result = ((x-x0)/1.5)^2 + ((y-y0)/1.1573)^2 - 1;
elseif (i == 13)
x0 = 17;
y0 = 9.25;
result = ((x-x0)/3)^2 + ((y-y0)/2.75)^2 - 1;
end
d06ba example results
Analysis of the boundary created:
The boundary mesh contains 332 vertices and 332 edges
There are 4 components comprising the boundary:
The 1-st component contains 4 lines in anticlockwise orientation
The 2-nd component contains 10 lines in clockwise orientation
The 3-rd component contains 12 lines in anticlockwise orientation
The 4-th component contains 19 lines in clockwise orientation
Complete mesh characteristics for Delauney-Voronoi mesh:
Number of vertices = 904
Number of elements = 1480
Complete mesh characteristics for advancing front mesh:
Number of vertices = 924
Number of elements = 1520
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015