NAG Toolbox: nag_mesh_2d_gen_front (d06ac)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{nvb}$ – int64int32nag_int scalar

The number of vertices in the input boundary mesh.

Constraint: $\mathbf{nvb}\ge 3$.

2:     $\mathrm{edge}\left(3,\mathbf{nedge}\right)$ – int64int32nag_int array

The specification of the boundary edges. $\mathbf{edge}\left(1,j\right)$ and $\mathbf{edge}\left(2,j\right)$ contain the vertex numbers of the two end points of the $j$th boundary edge. $\mathbf{edge}\left(3,j\right)$ is a user-supplied tag for the $j$th boundary edge and is not used by nag_mesh_2d_gen_front (d06ac).

Constraint: $1\le \mathbf{edge}\left(\mathit{i},\mathit{j}\right)\le \mathbf{nvb}$ and $\mathbf{edge}\left(1,\mathit{j}\right)\ne \mathbf{edge}\left(2,\mathit{j}\right)$, for $\mathit{i}=1,2$ and $\mathit{j}=1,2,\dots ,\mathbf{nedge}$.

3:     $\mathrm{coor}\left(2,\mathbf{nvmax}\right)$ – double array

$\mathbf{coor}\left(1,\mathit{i}\right)$ contains the $x$ coordinate of the $\mathit{i}$th input boundary mesh vertex, for $\mathit{i}=1,2,\dots ,\mathbf{nvb}$. $\mathbf{coor}\left(1,\mathit{i}\right)$ contains the $x$ coordinate of the $\left(\mathit{i}-\mathbf{nvb}\right)$th fixed interior vertex, for $\mathit{i}=\mathbf{nvb}+1,\dots ,\mathbf{nvb}+\mathbf{nvint}$. For boundary and interior vertices, $\mathbf{coor}\left(2,\mathit{i}\right)$ contains the corresponding $y$ coordinate, for $\mathit{i}=1,2,\dots ,\mathbf{nvb}+\mathbf{nvint}$.

4:     $\mathrm{weight}\left(:\right)$ – double array

The dimension of the array weight must be at least $\max \left(1,\mathbf{nvint}\right)$

The weight of fixed interior vertices. It is the diameter of triangles (length of the longer edge) created around each of the given interior vertices.

Constraint: if $\mathbf{nvint}>0$, $\mathbf{weight}\left(\mathit{i}\right)>0.0$, for $\mathit{i}=1,2,\dots ,\mathbf{nvint}$.

5:     $\mathrm{itrace}$ – int64int32nag_int scalar

The level of trace information required from nag_mesh_2d_gen_front (d06ac).

$\mathbf{itrace}\le 0$

No output is generated.

$\mathbf{itrace}\ge 1$

Output from the meshing solver is printed on the current advisory message unit (see nag_file_set_unit_advisory (x04ab)). This output contains details of the vertices and triangles generated by the process.

You are advised to set $\mathbf{itrace}=0$, unless you are experienced with finite element mesh generation.

Optional Input Parameters

1:     $\mathrm{nvint}$ – int64int32nag_int scalar

Default: the dimension of the array weight.

The number of fixed interior mesh vertices to which a weight will be applied.

Constraint: $\mathbf{nvint}\ge 0$.

2:     $\mathrm{nvmax}$ – int64int32nag_int scalar

Default: the dimension of the array coor.

The maximum number of vertices in the mesh to be generated.

Constraint: $\mathbf{nvmax}\ge \mathbf{nvb}+\mathbf{nvint}$.

3:     $\mathrm{nedge}$ – int64int32nag_int scalar

Default: the dimension of the array edge.

The number of boundary edges in the input mesh.

Constraint: $\mathbf{nedge}\ge 1$.

Output Parameters

1:     $\mathrm{nv}$ – int64int32nag_int scalar

The total number of vertices in the output mesh (including both boundary and interior vertices). If $\mathbf{nvb}+\mathbf{nvint}=\mathbf{nvmax}$, no interior vertices will be generated and $\mathbf{nv}=\mathbf{nvmax}$.

2:     $\mathrm{nelt}$ – int64int32nag_int scalar

The number of triangular elements in the mesh.

3:     $\mathrm{coor}\left(2,\mathbf{nvmax}\right)$ – double array

$\mathbf{coor}\left(1,\mathit{i}\right)$ will contain the $x$ coordinate of the $\left(\mathit{i}-\mathbf{nvb}-\mathbf{nvint}\right)$th generated interior mesh vertex, for $\mathit{i}=\mathbf{nvb}+\mathbf{nvint}+1,\dots ,\mathbf{nv}$; while $\mathbf{coor}\left(2,i\right)$ will contain the corresponding $y$ coordinate. The remaining elements are unchanged.

4:     $\mathrm{conn}\left(3,2\times \mathbf{nvmax}+5\right)$ – int64int32nag_int array

The connectivity of the mesh between triangles and vertices. For each triangle $\mathit{j}$, $\mathbf{conn}\left(\mathit{i},\mathit{j}\right)$ gives the indices of its three vertices (in anticlockwise order), for $\mathit{i}=1,2,3$ and $\mathit{j}=1,2,\dots ,\mathbf{nelt}$.

5:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

   $\mathbf{ifail}=1$

On entry,	$\mathbf{nvb}<3$,
or	$\mathbf{nvint}<0$,
or	$\mathbf{nvb}+\mathbf{nvint}>\mathbf{nvmax}$,
or	$\mathbf{nedge}<1$,
or	$\mathbf{edge}\left(i,j\right)<1$ or $\mathbf{edge}\left(i,j\right)>\mathbf{nvb}$, for some $i=1,2$ and $j=1,2,\dots ,\mathbf{nedge}$,
or	$\mathbf{edge}\left(1,j\right)=\mathbf{edge}\left(2,j\right)$, for some $j=1,2,\dots ,\mathbf{nedge}$,
or	if $\mathbf{nvint}>0$, $\mathbf{weight}\left(i\right)\le 0.0$, for some $i=1,2,\dots ,\mathbf{nvint}$;
or	$\mathit{lrwork}<12\times \mathbf{nvmax}+30015$,
or	$\mathit{liwork}<8\times \mathbf{nedge}+53\times \mathbf{nvmax}+2\times \mathbf{nvb}+10078$.

   $\mathbf{ifail}=2$

An error has occurred during the generation of the interior mesh. Check the definition of the boundary (arguments coor and edge) as well as the orientation of the boundary (especially in the case of a multiple connected component boundary). Setting $\mathbf{itrace}>0$ may provide more details.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Example

Open in the MATLAB editor: d06ac_example

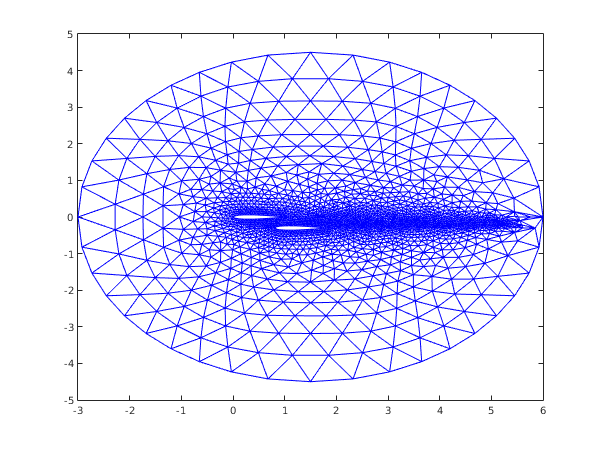
function d06ac_example


fprintf('d06ac example results\n\n');

% The characteristic points of the boundary mesh
coorch = [0, 1, -3, 6,  0.8,  1.8, 1.5,  1.5;
          0, 0,  0, 0, -0.3, -0.3, 4.5, -4.5];
coorus = zeros(2,100);
% The lines of the boundary mesh
blines = [int64(21), 21, 11, 11, 21, 21, 11, 11;
                   2,   1,  3,  4,  6,  5,  7,  8;
                   1,   2,  8,  7,  5,  6,  3,  4;
                   1,   2,  3,  3,  4,  5,  3,  3];
rate = ones(8,1);

% The number of connected components to the boundary
ncomp = int64(3);
% Number and direction of lines per contour
nlcomp = [int64(-2), 4, -2];
% List of line numbers
lcomp = [int64(1), 2, 3, 8, 4, 7, 5, 6];

user = struct('x0', 1.5, 'y0', 0, 'radius', 4.5, 'x1', 0.8, 'y1', -0.3);

nvmax = int64(2000);
nedmx = int64(200);
itrace = int64(0);


[nvb, coor, nedge, edge, user, ifail] = ...
d06ba( ...
       coorch, blines, @fbnd, coorus, rate, nlcomp, lcomp, nvmax, ...
       nedmx, itrace, 'user', user);
fprintf('\nBoundary mesh characteristics:\n');
fprintf('  nvb   = %d\n', nvb);
fprintf('  nedge = %d\n', nedge);

% Generation of interior vertices for the wake of the first naca
nvint  = 40;
nvint2 = 20;
dnvint = 5/(nvint2+1);
weight = ones(nvint,1)/nvint2;
for i=1:nvint2
  coor(1, nvb+i) = 1+i*dnvint;
end
% ... for the wake of the second naca
for i = nvint2+1:nvint
  coor(1, double(nvb)+i) = 1.8 + (i-nvint2)*dnvint;
  coor(2, double(nvb)+i) = -0.3;
end

% Call the 2D advancing front mesh generator.  Note only pass relevant
% portion of edge
[nv, nelt, coor, conn, ifail] = ...
d06ac( ...
       nvb, edge(:,1:nedge), coor, weight, itrace);

fprintf('\nComplete mesh characteristics:\n');
fprintf('  nv    = %d\n', nv);
fprintf('  nelt  = %d\n', nelt);

% Plot mesh
fig1 = figure;
triplot(transpose(double(conn(:,1:nelt))), coor(1,:), coor(2,:));


function [result, user] = fbnd(i, x, y, user)

  result = 0;
  c = 1.008930411365;
  p4 = @(x) 0.6*( 0.2969*sqrt(c*x) - 0.126*c*x - 0.3516*(c*x)^2 + ...
		  0.2843*(c*x)^3 - 0.1015*(c*x)^4 ); 
  if (i==1)
    % upper naca0012 wing beginning at the origin
    result = p4(x) -c*y;
  elseif (i==2)
    % lower naca0012 wing beginning at the origin
    result = p4(x) + c*y;
  elseif (i==3)
    result = (x-user.x0)^2 + (y-user.y0)^2 - user.radius^2;
  elseif (i==4)
    % upper naca0012 wing beginning at (user.x1;user.y1)
    result = p4(x-user.x1) - c*(y-user.y1);
  elseif (i==5)
    % lower naca0012 wing beginning at (user.x1;user.y1)
    result = p4(x-user.x1) + c*(y-user.y1);
  end

d06ac example results


Boundary mesh characteristics:
  nvb   = 120
  nedge = 120

Complete mesh characteristics:
  nv    = 1894
  nelt  = 3664