nag_pde_1d_parab_dae_coll (d03pj) integrates a system of linear or nonlinear parabolic partial differential equations (PDEs), in one space variable with scope for coupled ordinary differential equations (ODEs). The spatial discretization is performed using a Chebyshev

C^{0}

collocation method, and the method of lines is employed to reduce the PDEs to a system of ODEs. The resulting system is solved using a backward differentiation formula (BDF) method or a Theta method (switching between Newton's method and functional iteration).

Syntax

[ts, u, x, rsave, isave, ind, user, cwsav, lwsav, iwsav, rwsav, ifail] = d03pj(npde, m, ts, tout, pdedef, bndary, u, xbkpts, npoly, npts, ncode, odedef, xi, uvinit, rtol, atol, itol, norm_p, laopt, algopt, rsave, isave, itask, itrace, ind, cwsav, lwsav, iwsav, rwsav, 'nbkpts', nbkpts, 'nxi', nxi, 'neqn', neqn, 'user', user)

[ts, u, x, rsave, isave, ind, user, cwsav, lwsav, iwsav, rwsav, ifail] = nag_pde_1d_parab_dae_coll(npde, m, ts, tout, pdedef, bndary, u, xbkpts, npoly, npts, ncode, odedef, xi, uvinit, rtol, atol, itol, norm_p, laopt, algopt, rsave, isave, itask, itrace, ind, cwsav, lwsav, iwsav, rwsav, 'nbkpts', nbkpts, 'nxi', nxi, 'neqn', neqn, 'user', user)

Note: the interface to this routine has changed since earlier releases of the toolbox:

At Mark 22:

lrsave and lisave were removed from the interface

Description

nag_pde_1d_parab_dae_coll (d03pj) integrates the system of parabolic-elliptic equations and coupled ODEs

\sum_{j = 1}^{npde} P_{i, j} \frac{\partial U_{j}}{\partial t} + Q_{i} = x^{- m} \frac{\partial}{\partial x} (x^{m} R_{i}), i = 1, 2, \dots, npde, a \leq x \leq b, t \geq t_{0},

(1)

F_{i} (t, V, \dot{V}, ξ, U^{*}, U_{x}^{*}, R^{*}, U_{t}^{*}, U_{x t}^{*}) = 0, i = 1, 2, \dots, ncode,

(2)

where (1) defines the PDE part and (2) generalizes the coupled ODE part of the problem.

In (1),

P_{i, j}

and

R_{i}

depend on

x

t

U

U_{x}

, and

V

;

Q_{i}

depends on

x

t

U

U_{x}

V

and linearly on

\dot{V}

. The vector

U

is the set of PDE solution values

U (x, t) = {[U_{1} (x, t), \dots, U_{npde} (x, t)]}^{T},

and the vector

U_{x}

is the partial derivative with respect to

x

. Note that

P_{i, j}

Q_{i}

and

R_{i}

must not depend on

\frac{\partial U}{\partial t}

. The vector

V

is the set of ODE solution values

V (t) = {[V_{1} (t), \dots, V_{ncode} (t)]}^{T},

and

\dot{V}

denotes its derivative with respect to time.

In (2),

ξ

represents a vector of

n_{ξ}

spatial coupling points at which the ODEs are coupled to the PDEs. These points may or may not be equal to some of the PDE spatial mesh points.

U^{*}

U_{x}^{*}

R^{*}

U_{t}^{*}

and

U_{x t}^{*}

are the functions

U

U_{x}

R

U_{t}

and

U_{x t}

evaluated at these coupling points. Each

F_{i}

may only depend linearly on time derivatives. Hence the equation (2) may be written more precisely as

F = G - A \dot{V} - B (\begin{matrix} U_{t}^{*} \\ U_{x t}^{*} \end{matrix}),

(3)

where

F = {[F_{1}, \dots, F_{ncode}]}^{T}

G

is a vector of length ncode,

A

is an ncode by ncode matrix,

B

is an ncode by

(n_{ξ} \times npde)

matrix and the entries in

G

A

and

B

may depend on

t

ξ

U^{*}

U_{x}^{*}

and

V

. In practice you need only supply a vector of information to define the ODEs and not the matrices

A

and

B

. (See Arguments for the specification of odedef.)

The integration in time is from

t_{0}

t_{out}

, over the space interval

a \leq x \leq b

, where

a = x_{1}

and

b = x_{nbkpts}

are the leftmost and rightmost of a user-defined set of break-points

x_{1}, x_{2}, \dots, x_{nbkpts}

. The coordinate system in space is defined by the value of

m

;

m = 0

for Cartesian coordinates,

m = 1

for cylindrical polar coordinates and

m = 2

for spherical polar coordinates.

The PDE system which is defined by the functions

P_{i, j}

Q_{i}

and

R_{i}

must be specified in pdedef.

The initial values of the functions

U (x, t)

and

V (t)

must be given at

t = t_{0}

. These values are calculated in uvinit.

The functions

R_{i}

which may be thought of as fluxes, are also used in the definition of the boundary conditions. The boundary conditions must have the form

β_{i} (x, t) R_{i} (x, t, U, U_{x}, V) = γ_{i} (x, t, U, U_{x}, V, \dot{V}), i = 1, 2, \dots, npde,

(4)

where

x = a

x = b

. The functions

γ_{i}

may only depend linearly on

\dot{V}

The boundary conditions must be specified in bndary.

The algebraic-differential equation system which is defined by the functions

F_{i}

must be specified in odedef. You must also specify the coupling points

ξ

in the array xi. Thus, the problem is subject to the following restrictions:

(i)	in (1), ${\dot{V}}_{j} (t)$ , for $j = 1, 2, \dots, ncode$ , may only appear linearly in the functions $Q_{i}$ , for $i = 1, 2, \dots, npde$ , with a similar restriction for $γ$ ;
(ii)	$P_{i, j}$ and the flux $R_{i}$ must not depend on any time derivatives;
(iii)	$t_{0} < t_{out}$ , so that integration is in the forward direction;
(iv)	the evaluation of the functions $P_{i, j}$ , $Q_{i}$ and $R_{i}$ is done at both the break-points and internally selected points for each element in turn, that is $P_{i, j}$ , $Q_{i}$ and $R_{i}$ are evaluated twice at each break-point. Any discontinuities in these functions must therefore be at one or more of the mesh points;
(v)	at least one of the functions $P_{i, j}$ must be nonzero so that there is a time derivative present in the PDE problem;
(vi)	if $m > 0$ and $x_{1} = 0.0$ , which is the left boundary point, then it must be ensured that the PDE solution is bounded at this point. This can be done either by specifying the solution at $x = 0.0$ or by specifying a zero flux there, that is $β_{i} = 1.0$ and $γ_{i} = 0.0$ .

The parabolic equations are approximated by a system of ODEs in time for the values of

U_{i}

at the mesh points. This ODE system is obtained by approximating the PDE solution between each pair of break-points by a Chebyshev polynomial of degree npoly. The interval between each pair of break-points is treated by nag_pde_1d_parab_dae_coll (d03pj) as an element, and on this element, a polynomial and its space and time derivatives are made to satisfy the system of PDEs at

npoly - 1

spatial points, which are chosen internally by the code and the break-points. The user-defined break-points and the internally selected points together define the mesh. The smallest value that npoly can take is one, in which case, the solution is approximated by piecewise linear polynomials between consecutive break-points and the method is similar to an ordinary finite element method.

In total there are

(nbkpts - 1) \times npoly + 1

mesh points in the spatial direction, and

npde \times ((nbkpts - 1) \times npoly + 1) + ncode

ODEs in the time direction; one ODE at each break-point for each PDE component,

npoly - 1

ODEs for each PDE component between each pair of break-points, and ncode coupled ODEs. The system is then integrated forwards in time using a Backward Differentiation Formula (BDF) method or a Theta method.

References

Berzins M (1990) Developments in the NAG Library software for parabolic equations Scientific Software Systems (eds J C Mason and M G Cox) 59–72 Chapman and Hall

Berzins M and Dew P M (1991) Algorithm 690: Chebyshev polynomial software for elliptic-parabolic systems of PDEs ACM Trans. Math. Software 17 178–206

Berzins M, Dew P M and Furzeland R M (1988) Software tools for time-dependent equations in simulation and optimization of large systems Proc. IMA Conf. Simulation and Optimization (ed A J Osiadcz) 35–50 Clarendon Press, Oxford

Berzins M and Furzeland R M (1992) An adaptive theta method for the solution of stiff and nonstiff differential equations Appl. Numer. Math. 9 1–19

Zaturska N B, Drazin P G and Banks W H H (1988) On the flow of a viscous fluid driven along a channel by a suction at porous walls Fluid Dynamics Research 4

Parameters

Compulsory Input Parameters

1: $npde$ – int64int32nag_int scalar

The number of PDEs to be solved.

Constraint:

npde \geq 1

2: $m$ – int64int32nag_int scalar

The coordinate system used:

$m = 0$: Indicates Cartesian coordinates.
$m = 1$: Indicates cylindrical polar coordinates.
$m = 2$: Indicates spherical polar coordinates.

Constraint:

m = 0

1

2

3: $ts$ – double scalar

The initial value of the independent variable

t

Constraint:

ts < tout

4: $tout$ – double scalar

The final value of

t

to which the integration is to be carried out.

5: $pdedef$ – function handle or string containing name of m-file

pdedef must compute the functions

P_{i, j}

Q_{i}

and

R_{i}

which define the system of PDEs. The functions may depend on

x

t

U

U_{x}

and

V

;

Q_{i}

may depend linearly on

\dot{V}

. The functions must be evaluated at a set of points.

[p, q, r, ires, user] = pdedef(npde, t, x, nptl, u, ux, ncode, v, vdot, ires, user)

Input Parameters

1: $npde$ – int64int32nag_int scalar: The number of PDEs in the system.
2: $t$ – double scalar: The current value of the independent variable $t$ .
3: $x (nptl)$ – double array: Contains a set of mesh points at which $P_{i, j}$ , $Q_{i}$ and $R_{i}$ are to be evaluated. $x (1)$ and $x (nptl)$ contain successive user-supplied break-points and the elements of the array will satisfy $x (1) < x (2) < \dots < x (nptl)$ .
4: $nptl$ – int64int32nag_int scalar: The number of points at which evaluations are required (the value of $npoly + 1$ ).
5: $u (npde, nptl)$ – double array: $u (i, j)$ contains the value of the component $U_{i} (x, t)$ where $x = x (j)$ , for $i = 1, 2, \dots, npde$ and $j = 1, 2, \dots, nptl$ .
6: $ux (npde, nptl)$ – double array: $ux (i, j)$ contains the value of the component $\frac{\partial U_{i} (x, t)}{\partial x}$ where $x = x (j)$ , for $i = 1, 2, \dots, npde$ and $j = 1, 2, \dots, nptl$ .
7: $ncode$ – int64int32nag_int scalar: The number of coupled ODEs in the system.
8: $v (ncode)$ – double array: If $ncode > 0$ , $v (i)$ contains the value of the component $V_{i} (t)$ , for $i = 1, 2, \dots, ncode$ .
9: $vdot (ncode)$ – double array: If $ncode > 0$ , $vdot (i)$ contains the value of component ${\dot{V}}_{i} (t)$ , for $i = 1, 2, \dots, ncode$ .
Note: ${\dot{V}}_{i} (t)$ , for $i = 1, 2, \dots, ncode$ , may only appear linearly in $Q_{j}$ , for $j = 1, 2, \dots, npde$ .
10: $ires$ – int64int32nag_int scalar: Set to $- 1 or 1$ .
11: $user$ – Any MATLAB object: pdedef is called from nag_pde_1d_parab_dae_coll (d03pj) with the object supplied to nag_pde_1d_parab_dae_coll (d03pj).

Output Parameters

1: $p (npde, npde, nptl)$ – double array

p (i, j, k)

must be set to the value of

P_{i, j} (x, t, U, U_{x}, V)

where

x = x (k)

, for

i = 1, 2, \dots, npde

j = 1, 2, \dots, npde

and

k = 1, 2, \dots, nptl

2: $q (npde, nptl)$ – double array

q (i, j)

must be set to the value of

Q_{i} (x, t, U, U_{x}, V, \dot{V})

where

x = x (j)

, for

i = 1, 2, \dots, npde

and

j = 1, 2, \dots, nptl

3: $r (npde, nptl)$ – double array

r (i, j)

must be set to the value of

R_{i} (x, t, U, U_{x}, V)

where

x = x (i)

, for

i = 1, 2, \dots, npde

and

j = 1, 2, \dots, nptl

4: $ires$ – int64int32nag_int scalar

Should usually remain unchanged. However, you may set ires to force the integration function to take certain actions as described below:

$ires = 2$: Indicates to the integrator that control should be passed back immediately to the calling (sub)routine with the error indicator set to $ifail = 6$ .
$ires = 3$: Indicates to the integrator that the current time step should be abandoned and a smaller time step used instead. You may wish to set $ires = 3$ when a physically meaningless input or output value has been generated. If you consecutively set $ires = 3$ , then nag_pde_1d_parab_dae_coll (d03pj) returns to the calling function with the error indicator set to $ifail = 4$ .

5: $user$ – Any MATLAB object

6: $bndary$ – function handle or string containing name of m-file

bndary must compute the functions

β_{i}

and

γ_{i}

which define the boundary conditions as in equation (4).

[beta, gamma, ires, user] = bndary(npde, t, u, ux, ncode, v, vdot, ibnd, ires, user)

Input Parameters

1: $npde$ – int64int32nag_int scalar

The number of PDEs in the system.

2: $t$ – double scalar

The current value of the independent variable

t

3: $u (npde)$ – double array

u (i)

contains the value of the component

U_{i} (x, t)

at the boundary specified by ibnd, for

i = 1, 2, \dots, npde

4: $ux (npde)$ – double array

ux (i)

contains the value of the component

\frac{\partial U_{i} (x, t)}{\partial x}

at the boundary specified by ibnd, for

i = 1, 2, \dots, npde

5: $ncode$ – int64int32nag_int scalar

The number of coupled ODEs in the system.

6: $v (ncode)$ – double array

ncode > 0

v (i)

contains the value of the component

V_{i} (t)

, for

i = 1, 2, \dots, ncode

7: $vdot (ncode)$ – double array

ncode > 0

vdot (i)

contains the value of component

{\dot{V}}_{i} (t)

, for

i = 1, 2, \dots, ncode

Note:

{\dot{V}}_{i} (t)

, for

i = 1, 2, \dots, ncode

, may only appear linearly in

Q_{j}

, for

j = 1, 2, \dots, npde

8: $ibnd$ – int64int32nag_int scalar

Specifies which boundary conditions are to be evaluated.

$ibnd = 0$: bndary must set up the coefficients of the left-hand boundary, $x = a$ .
$ibnd \neq 0$: bndary must set up the coefficients of the right-hand boundary, $x = b$ .

9: $ires$ – int64int32nag_int scalar

Set to

- 1 ​ or ​ 1

10: $user$ – Any MATLAB object

bndary is called from nag_pde_1d_parab_dae_coll (d03pj) with the object supplied to nag_pde_1d_parab_dae_coll (d03pj).

Output Parameters

1: $beta (npde)$ – double array

beta (i)

must be set to the value of

β_{i} (x, t)

at the boundary specified by ibnd, for

i = 1, 2, \dots, npde

2: $gamma (npde)$ – double array

gamma (i)

must be set to the value of

γ_{i} (x, t, U, U_{x}, V, \dot{V})

at the boundary specified by ibnd, for

i = 1, 2, \dots, npde

3: $ires$ – int64int32nag_int scalar

Should usually remain unchanged. However, you may set ires to force the integration function to take certain actions as described below:

$ires = 2$: Indicates to the integrator that control should be passed back immediately to the calling (sub)routine with the error indicator set to $ifail = 6$ .
$ires = 3$: Indicates to the integrator that the current time step should be abandoned and a smaller time step used instead. You may wish to set $ires = 3$ when a physically meaningless input or output value has been generated. If you consecutively set $ires = 3$ , then nag_pde_1d_parab_dae_coll (d03pj) returns to the calling function with the error indicator set to $ifail = 4$ .

4: $user$ – Any MATLAB object

7: $u (neqn)$ – double array

ind = 1

the value of u must be unchanged from the previous call.

8: $xbkpts (nbkpts)$ – double array

The values of the break-points in the space direction.

xbkpts (1)

must specify the left-hand boundary,

a

, and

xbkpts (nbkpts)

must specify the right-hand boundary,

b

Constraint:

xbkpts (1) < xbkpts (2) < \dots < xbkpts (nbkpts)

9: $npoly$ – int64int32nag_int scalar

The degree of the Chebyshev polynomial to be used in approximating the PDE solution between each pair of break-points.

Constraint:

1 \leq npoly \leq 49

10: $npts$ – int64int32nag_int scalar

The number of mesh points in the interval

[a, b]

Constraint:

npts = (nbkpts - 1) \times npoly + 1

11: $ncode$ – int64int32nag_int scalar

The number of coupled ODE components.

Constraint:

ncode \geq 0

12: $odedef$ – function handle or string containing name of m-file

odedef must evaluate the functions

F

, which define the system of ODEs, as given in (3).

If you wish to compute the solution of a system of PDEs only (

ncode = 0

), odedef must be the string nag_pde_1d_parab_remesh_fd_dummy_odedef (d53pck).

[f, ires, user] = odedef(npde, t, ncode, v, vdot, nxi, xi, ucp, ucpx, rcp, ucpt, ucptx, ires, user)

Input Parameters

1: $npde$ – int64int32nag_int scalar

The number of PDEs in the system.

2: $t$ – double scalar

The current value of the independent variable

t

3: $ncode$ – int64int32nag_int scalar

The number of coupled ODEs in the system.

4: $v (ncode)$ – double array

ncode > 0

v (i)

contains the value of the component

V_{i} (t)

, for

i = 1, 2, \dots, ncode

5: $vdot (ncode)$ – double array

ncode > 0

vdot (i)

contains the value of component

{\dot{V}}_{i} (t)

, for

i = 1, 2, \dots, ncode

6: $nxi$ – int64int32nag_int scalar

The number of ODE/PDE coupling points.

7: $xi (nxi)$ – double array

nxi > 0

xi (i)

contains the ODE/PDE coupling points,

ξ_{i}

, for

i = 1, 2, \dots, nxi

8: $ucp (npde :)$ – double array

The second dimension of the array ucp must be at least

\max (1, nxi)

nxi > 0

ucp (i, j)

contains the value of

U_{i} (x, t)

at the coupling point

x = ξ_{j}

, for

i = 1, 2, \dots, npde

and

j = 1, 2, \dots, nxi

9: $ucpx (npde :)$ – double array

The second dimension of the array ucpx must be at least

\max (1, nxi)

nxi > 0

ucpx (i, j)

contains the value of

\frac{\partial U_{i} (x, t)}{\partial x}

at the coupling point

x = ξ_{j}

, for

i = 1, 2, \dots, npde

and

j = 1, 2, \dots, nxi

10: $rcp (npde :)$ – double array

The second dimension of the array rcp must be at least

\max (1, nxi)

rcp (i, j)

contains the value of the flux

R_{i}

at the coupling point

x = ξ_{j}

, for

i = 1, 2, \dots, npde

and

j = 1, 2, \dots, nxi

11: $ucpt (npde :)$ – double array

The second dimension of the array ucpt must be at least

\max (1, nxi)

nxi > 0

ucpt (i, j)

contains the value of

\frac{\partial U_{i}}{\partial t}

at the coupling point

x = ξ_{j}

, for

i = 1, 2, \dots, npde

and

j = 1, 2, \dots, nxi

12: $ucptx (npde :)$ – double array

The second dimension of the array ucptx must be at least

\max (1, nxi)

ucptx (i, j)

contains the value of

\frac{\partial^{2} U_{i}}{\partial x \partial t}

at the coupling point

x = ξ_{j}

, for

i = 1, 2, \dots, npde

and

j = 1, 2, \dots, nxi

13: $ires$ – int64int32nag_int scalar

The form of

F

that must be returned in the array f.

$ires = 1$: Equation (5) must be used.
$ires = - 1$: Equation (6) must be used.

14: $user$ – Any MATLAB object

odedef is called from nag_pde_1d_parab_dae_coll (d03pj) with the object supplied to nag_pde_1d_parab_dae_coll (d03pj).

Output Parameters

1: $f (ncode)$ – double array

f (i)

must contain the

i

th component of

F

, for

i = 1, 2, \dots, ncode

, where

F

is defined as

F = G - A \dot{V} - B (\begin{matrix} U_{t}^{*} \\ U_{x t}^{*} \end{matrix}),

(5)

F = - A \dot{V} - B (\begin{matrix} U_{t}^{*} \\ U_{x t}^{*} \end{matrix}) .

(6)

The definition of

F

is determined by the input value of ires.

2: $ires$ – int64int32nag_int scalar

Should usually remain unchanged. However, you may reset ires to force the integration function to take certain actions as described below:

$ires = 2$: Indicates to the integrator that control should be passed back immediately to the calling (sub)routine with the error indicator set to $ifail = 6$ .
$ires = 3$: Indicates to the integrator that the current time step should be abandoned and a smaller time step used instead. You may wish to set $ires = 3$ when a physically meaningless input or output value has been generated. If you consecutively set $ires = 3$ , then nag_pde_1d_parab_dae_coll (d03pj) returns to the calling function with the error indicator set to $ifail = 4$ .

3: $user$ – Any MATLAB object

13: $xi (:)$ – double array

The dimension of the array xi must be at least

\max (1, nxi)

xi (i)

, for

i = 1, 2, \dots, nxi

, must be set to the ODE/PDE coupling points.

Constraint:

xbkpts (1) \leq xi (1) < xi (2) < \dots < xi (nxi) \leq xbkpts (nbkpts)

14: $uvinit$ – function handle or string containing name of m-file

uvinit must compute the initial values of the PDE and the ODE components

U_{i} (x_{j}, t_{0})

, for

i = 1, 2, \dots, npde

and

j = 1, 2, \dots, npts

, and

V_{k} (t_{0})

, for

k = 1, 2, \dots, ncode

[u, v, user] = uvinit(npde, npts, x, ncode, user)

Input Parameters

1: $npde$ – int64int32nag_int scalar: The number of PDEs in the system.
2: $npts$ – int64int32nag_int scalar: The number of mesh points in the interval $[a, b]$ .
3: $x (npts)$ – double array: $x (i)$ , for $i = 1, 2, \dots, npts$ , contains the current values of the space variable $x_{i}$ .
4: $ncode$ – int64int32nag_int scalar: The number of coupled ODEs in the system.
5: $user$ – Any MATLAB object: uvinit is called from nag_pde_1d_parab_dae_coll (d03pj) with the object supplied to nag_pde_1d_parab_dae_coll (d03pj).

Output Parameters

1: $u (npde, npts)$ – double array: If $nxi > 0$ , $u (i, j)$ contains the value of the component $U_{i} (x_{j}, t_{0})$ , for $i = 1, 2, \dots, npde$ and $j = 1, 2, \dots, npts$ .
2: $v (ncode)$ – double array: $v (i)$ contains the value of component $V_{i} (t_{0})$ , for $i = 1, 2, \dots, ncode$ .
3: $user$ – Any MATLAB object

15: $rtol (:)$ – double array

The dimension of the array rtol must be at least

1

itol = 1

2

and at least

neqn

itol = 3

4

The relative local error tolerance.

Constraint:

rtol (i) \geq 0.0

for all relevant

i

16: $atol (:)$ – double array

The dimension of the array atol must be at least

1

itol = 1

3

and at least

neqn

itol = 2

4

The absolute local error tolerance.

Constraint:

atol (i) \geq 0.0

for all relevant

i

Note: corresponding elements of rtol and atol cannot both be

0.0

17: $itol$ – int64int32nag_int scalar

A value to indicate the form of the local error test. itol indicates to nag_pde_1d_parab_dae_coll (d03pj) whether to interpret either or both of rtol or atol as a vector or scalar. The error test to be satisfied is

‖e_{i} / w_{i}‖ < 1.0

, where

w_{i}

is defined as follows:

itol	rtol	atol	$w_{i}$
1	scalar	scalar	$rtol (1) \times \|U_{i}\| + atol (1)$
2	scalar	vector	$rtol (1) \times \|U_{i}\| + atol (i)$
3	vector	scalar	$rtol (i) \times \|U_{i}\| + atol (1)$
4	vector	vector	$rtol (i) \times \|U_{i}\| + atol (i)$

In the above,

e_{i}

denotes the estimated local error for the

i

th component of the coupled PDE/ODE system in time,

u (i)

, for

i = 1, 2, \dots, neqn

The choice of norm used is defined by the argument norm_p.

Constraint:

1 \leq itol \leq 4

18: $norm_p$ – string (length ≥ 1)

The type of norm to be used.

$norm_p ='M'$: Maximum norm.
$norm_p ='A'$: Averaged $L_{2}$ norm.

u_{norm}

denotes the norm of the vector u of length neqn, then for the averaged

L_{2}

norm

u_{norm} = \sqrt{\frac{1}{neqn} \sum_{i = 1}^{neqn} {(u (i) / w_{i})}^{2}},

while for the maximum norm

u_{norm} = \max_{i} |u (i) / w_{i}| .

See the description of itol for the formulation of the weight vector

w

Constraint:

norm_p ='M'

'A'

19: $laopt$ – string (length ≥ 1)

The type of matrix algebra required.

$laopt ='F'$: Full matrix methods to be used.
$laopt ='B'$: Banded matrix methods to be used.
$laopt ='S'$: Sparse matrix methods to be used.

Constraint:

laopt ='F'

'B'

'S'

Note: you are recommended to use the banded option when no coupled ODEs are present (i.e.,

ncode = 0

20: $algopt (30)$ – double array

May be set to control various options available in the integrator. If you wish to employ all the default options, then

algopt (1)

should be set to

0.0

. Default values will also be used for any other elements of algopt set to zero. The permissible values, default values, and meanings are as follows:

$algopt (1)$: Selects the ODE integration method to be used. If $algopt (1) = 1.0$ , a BDF method is used and if $algopt (1) = 2.0$ , a Theta method is used. The default value is $algopt (1) = 1.0$ .

algopt (1) = 2.0

, then

algopt (i)

, for

i = 2, 3, 4

are not used.

$algopt (2)$: Specifies the maximum order of the BDF integration formula to be used. $algopt (2)$ may be $1.0$ , $2.0$ , $3.0$ , $4.0$ or $5.0$ . The default value is $algopt (2) = 5.0$ .
$algopt (3)$: Specifies what method is to be used to solve the system of nonlinear equations arising on each step of the BDF method. If $algopt (3) = 1.0$ a modified Newton iteration is used and if $algopt (3) = 2.0$ a functional iteration method is used. If functional iteration is selected and the integrator encounters difficulty, then there is an automatic switch to the modified Newton iteration. The default value is $algopt (3) = 1.0$ .
$algopt (4)$: Specifies whether or not the Petzold error test is to be employed. The Petzold error test results in extra overhead but is more suitable when algebraic equations are present, such as $P_{i, j} = 0.0$ , for $j = 1, 2, \dots, npde$ , for some $i$ or when there is no ${\dot{V}}_{i} (t)$ dependence in the coupled ODE system. If $algopt (4) = 1.0$ , then the Petzold test is used. If $algopt (4) = 2.0$ , then the Petzold test is not used. The default value is $algopt (4) = 1.0$ .

algopt (1) = 1.0

, then

algopt (i)

, for

i = 5, 6, 7

, are not used.

$algopt (5)$: Specifies the value of Theta to be used in the Theta integration method. $0.51 \leq algopt (5) \leq 0.99$ . The default value is $algopt (5) = 0.55$ .
$algopt (6)$: Specifies what method is to be used to solve the system of nonlinear equations arising on each step of the Theta method. If $algopt (6) = 1.0$ , a modified Newton iteration is used and if $algopt (6) = 2.0$ , a functional iteration method is used. The default value is $algopt (6) = 1.0$ .
$algopt (7)$: Specifies whether or not the integrator is allowed to switch automatically between modified Newton and functional iteration methods in order to be more efficient. If $algopt (7) = 1.0$ , then switching is allowed and if $algopt (7) = 2.0$ , then switching is not allowed. The default value is $algopt (7) = 1.0$ .
$algopt (11)$: Specifies a point in the time direction, $t_{crit}$ , beyond which integration must not be attempted. The use of $t_{crit}$ is described under the argument itask. If $algopt (1) \neq 0.0$ , a value of $0.0$ for $algopt (11)$ , say, should be specified even if itask subsequently specifies that $t_{crit}$ will not be used.
$algopt (12)$: Specifies the minimum absolute step size to be allowed in the time integration. If this option is not required, $algopt (12)$ should be set to $0.0$ .
$algopt (13)$: Specifies the maximum absolute step size to be allowed in the time integration. If this option is not required, $algopt (13)$ should be set to $0.0$ .
$algopt (14)$: Specifies the initial step size to be attempted by the integrator. If $algopt (14) = 0.0$ , then the initial step size is calculated internally.
$algopt (15)$: Specifies the maximum number of steps to be attempted by the integrator in any one call. If $algopt (15) = 0.0$ , then no limit is imposed.
$algopt (23)$: Specifies what method is to be used to solve the nonlinear equations at the initial point to initialize the values of $U$ , $U_{t}$ , $V$ and $\dot{V}$ . If $algopt (23) = 1.0$ , a modified Newton iteration is used and if $algopt (23) = 2.0$ , functional iteration is used. The default value is $algopt (23) = 1.0$ .

algopt (29)

and

algopt (30)

are used only for the sparse matrix algebra option,

laopt ='S'

$algopt (29)$: Governs the choice of pivots during the decomposition of the first Jacobian matrix. It should lie in the range $0.0 < algopt (29) < 1.0$ , with smaller values biasing the algorithm towards maintaining sparsity at the expense of numerical stability. If $algopt (29)$ lies outside this range then the default value is used. If the functions regard the Jacobian matrix as numerically singular then increasing $algopt (29)$ towards $1.0$ may help, but at the cost of increased fill-in. The default value is $algopt (29) = 0.1$ .
$algopt (30)$: Is used as a relative pivot threshold during subsequent Jacobian decompositions (see $algopt (29)$ ) below which an internal error is invoked. If $algopt (30)$ is greater than $1.0$ no check is made on the pivot size, and this may be a necessary option if the Jacobian is found to be numerically singular (see $algopt (29)$ ). The default value is $algopt (30) = 0.0001$ .

21: $rsave (lrsave)$ – double array

ind = 0

, rsave need not be set on entry.

ind = 1

, rsave must be unchanged from the previous call to the function because it contains required information about the iteration.

22: $isave (lisave)$ – int64int32nag_int array

ind = 0

, isave need not be set on entry.

ind = 1

, isave must be unchanged from the previous call to the function because it contains required information about the iteration required for subsequent calls. In particular:

$isave (1)$: Contains the number of steps taken in time.
$isave (2)$: Contains the number of residual evaluations of the resulting ODE system used. One such evaluation involves computing the PDE functions at all the mesh points, as well as one evaluation of the functions in the boundary conditions.
$isave (3)$: Contains the number of Jacobian evaluations performed by the time integrator.
$isave (4)$: Contains the order of the ODE method last used in the time integration.
$isave (5)$: Contains the number of Newton iterations performed by the time integrator. Each iteration involves residual evaluation of the resulting ODE system followed by a back-substitution using the $L U$ decomposition of the Jacobian matrix.

23: $itask$ – int64int32nag_int scalar

Specifies the task to be performed by the ODE integrator.

$itask = 1$: Normal computation of output values u at $t = tout$ .
$itask = 2$: One step and return.
$itask = 3$: Stop at first internal integration point at or beyond $t = tout$ .
$itask = 4$: Normal computation of output values u at $t = tout$ but without overshooting $t = t_{crit}$ where $t_{crit}$ is described under the argument algopt.
$itask = 5$: Take one step in the time direction and return, without passing $t_{crit}$ , where $t_{crit}$ is described under the argument algopt.

Constraint:

itask = 1

2

3

4

5

24: $itrace$ – int64int32nag_int scalar

The level of trace information required from nag_pde_1d_parab_dae_coll (d03pj) and the underlying ODE solver. itrace may take the value

- 1

0

1

2

3

$itrace = - 1$: No output is generated.
$itrace = 0$: Only warning messages from the PDE solver are printed on the current error message unit (see nag_file_set_unit_error (x04aa)).
$itrace > 0$: Output from the underlying ODE solver is printed on the current advisory message unit (see nag_file_set_unit_advisory (x04ab)). This output contains details of Jacobian entries, the nonlinear iteration and the time integration during the computation of the ODE system.

itrace < - 1

, then

- 1

is assumed and similarly if

itrace > 3

, then

3

is assumed.

The advisory messages are given in greater detail as itrace increases. You are advised to set

itrace = 0

, unless you are experienced with Sub-chapter D02M–N.

25: $ind$ – int64int32nag_int scalar

Indicates whether this is a continuation call or a new integration.

$ind = 0$: Starts or restarts the integration in time.
$ind = 1$: Continues the integration after an earlier exit from the function. In this case, only the arguments tout and ifail should be reset between calls to nag_pde_1d_parab_dae_coll (d03pj).

Constraint:

ind = 0

1

26: $cwsav (10)$ – cell array of strings

27: $lwsav (100)$ – logical array

28: $iwsav (505)$ – int64int32nag_int array

29: $rwsav (1100)$ – double array

Optional Input Parameters

1: $nbkpts$ – int64int32nag_int scalar

Default: the dimension of the array xbkpts.

The number of break-points in the interval

[a, b]

Constraint:

nbkpts \geq 2

2: $nxi$ – int64int32nag_int scalar

Default: the dimension of the array xi.

The number of ODE/PDE coupling points.

Constraints:

if $ncode = 0$ , $nxi = 0$ ;
if $ncode > 0$ , $nxi \geq 0$ .

3: $neqn$ – int64int32nag_int scalar

Default: the dimension of the array u.

The number of ODEs in the time direction.

Constraint:

neqn = npde \times npts + ncode

4: $user$ – Any MATLAB object

user is not used by nag_pde_1d_parab_dae_coll (d03pj), but is passed to pdedef, bndary, odedef and uvinit. Note that for large objects it may be more efficient to use a global variable which is accessible from the m-files than to use user.

Output Parameters

1: $ts$ – double scalar

The value of

t

corresponding to the solution values in u. Normally

ts = tout

2: $u (neqn)$ – double array

The computed solution

U_{i} (x_{j}, t)

, for

i = 1, 2, \dots, npde

and

j = 1, 2, \dots, npts

, and

V_{k} (t)

, for

k = 1, 2, \dots, ncode

, evaluated at

t = ts

, as follows:

$u (npde \times (j - 1) + i)$ contain $U_{i} (x_{j}, t)$ , for $i = 1, 2, \dots, npde$ and $j = 1, 2, \dots, npts$ , and
$u (npts \times npde + i)$ contain $V_{i} (t)$ , for $i = 1, 2, \dots, ncode$ .

3: $x (npts)$ – double array

The mesh points chosen by nag_pde_1d_parab_dae_coll (d03pj) in the spatial direction. The values of x will satisfy

x (1) < x (2) < \dots < x (npts)

4: $rsave (lrsave)$ – double array

ind = 1

, rsave must be unchanged from the previous call to the function because it contains required information about the iteration.

5: $isave (lisave)$ – int64int32nag_int array

ind = 1

, isave must be unchanged from the previous call to the function because it contains required information about the iteration required for subsequent calls. In particular:

$isave (1)$: Contains the number of steps taken in time.
$isave (2)$: Contains the number of residual evaluations of the resulting ODE system used. One such evaluation involves computing the PDE functions at all the mesh points, as well as one evaluation of the functions in the boundary conditions.
$isave (3)$: Contains the number of Jacobian evaluations performed by the time integrator.
$isave (4)$: Contains the order of the ODE method last used in the time integration.
$isave (5)$: Contains the number of Newton iterations performed by the time integrator. Each iteration involves residual evaluation of the resulting ODE system followed by a back-substitution using the $L U$ decomposition of the Jacobian matrix.

6: $ind$ – int64int32nag_int scalar

ind = 1

7: $user$ – Any MATLAB object

8: $cwsav (10)$ – cell array of strings

9: $lwsav (100)$ – logical array

10: $iwsav (505)$ – int64int32nag_int array

11: $rwsav (1100)$ – double array

12: $ifail$ – int64int32nag_int scalar

ifail = 0

unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Errors or warnings detected by the function:

Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.

$ifail = 1$

On entry,	$tout - ts$ is too small,
or	$itask \neq 1$ , $2$ , $3$ , $4$ or $5$ ,
or	$m \neq 0$ , $1$ or $2$ ,
or	at least one of the coupling point in array xi is outside the interval [ $xbkpts (1), xbkpts (nbkpts)$ ],
or	$npts \neq (nbkpts - 1) \times npoly + 1$ ,
or	$nbkpts < 2$ ,
or	$npde \leq 0$ ,
or	$norm_p \neq'A'$ or $'M'$ ,
or	$itol \neq 1$ , $2$ , $3$ or $4$ ,
or	$npoly < 1$ or $npoly > 49$ ,
or	ncode and nxi are incorrectly defined,
or	$neqn \neq npde \times npts + ncode$ ,
or	$laopt \neq'F'$ , $'B'$ or $'S'$ ,
or	$ind \neq 0$ or $1$ ,
or	break-points $xbkpts (i)$ are badly ordered,
or	lrsave is too small,
or	lisave is too small,
or	the ODE integrator has not been correctly defined; check algopt argument,
or	either an element of rtol or $atol < 0.0$ ,
or	all the elements of rtol and atol are zero.

W $ifail = 2$: The underlying ODE solver cannot make any further progress, with the values of atol and rtol, across the integration range from the current point $t = ts$ . The components of u contain the computed values at the current point $t = ts$ .

W $ifail = 3$: In the underlying ODE solver, there were repeated error test failures on an attempted step, before completing the requested task, but the integration was successful as far as $t = ts$ . The problem may have a singularity, or the error requirement may be inappropriate.

$ifail = 4$: In setting up the ODE system, the internal initialization function was unable to initialize the derivative of the ODE system. This could be due to the fact that ires was repeatedly set to $3$ in at least pdedef, bndary or odedef, when the residual in the underlying ODE solver was being evaluated.

$ifail = 5$: In solving the ODE system, a singular Jacobian has been encountered. You should check your problem formulation.

W $ifail = 6$: When evaluating the residual in solving the ODE system, ires was set to $2$ in at least pdedef, bndary or odedef. Integration was successful as far as $t = ts$ .

$ifail = 7$: The values of atol and rtol are so small that the function is unable to start the integration in time.

$ifail = 8$: In one of pdedef, bndary or odedef, ires was set to an invalid value.

$ifail = 9$ (nag_ode_ivp_stiff_imp_revcom (d02nn)): A serious error has occurred in an internal call to the specified function. Check the problem specification and all arguments and array dimensions. Setting $itrace = 1$ may provide more information. If the problem persists, contact NAG.

W $ifail = 10$: The required task has been completed, but it is estimated that a small change in atol and rtol is unlikely to produce any change in the computed solution. (Only applies when you are not operating in one step mode, that is when $itask \neq 2$ or $5$ .)

$ifail = 11$: An error occurred during Jacobian formulation of the ODE system (a more detailed error description may be directed to the current error message unit).

$ifail = 12$: In solving the ODE system, the maximum number of steps specified in $algopt (15)$ have been taken.

W $ifail = 13$: Some error weights $w_{i}$ became zero during the time integration (see the description of itol). Pure relative error control ( $atol (i) = 0.0$ ) was requested on a variable (the $i$ th) which has become zero. The integration was successful as far as $t = ts$ .

$ifail = 14$: The flux function $R_{i}$ was detected as depending on time derivatives, which is not permissible.

$ifail = 15$: When using the sparse option, the value of lisave or lrsave was not sufficient (more detailed information may be directed to the current error message unit).

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.

$ifail = - 999$: Dynamic memory allocation failed.

Accuracy

nag_pde_1d_parab_dae_coll (d03pj) controls the accuracy of the integration in the time direction but not the accuracy of the approximation in space. The spatial accuracy depends on both the number of mesh points and on their distribution in space. In the time integration only the local error over a single step is controlled and so the accuracy over a number of steps cannot be guaranteed. You should therefore test the effect of varying the accuracy argument atol and rtol.

Further Comments

The argument specification allows you to include equations with only first-order derivatives in the space direction but there is no guarantee that the method of integration will be satisfactory for such systems. The position and nature of the boundary conditions in particular are critical in defining a stable problem.

The time taken depends on the complexity of the parabolic system and on the accuracy requested.

Example

This example provides a simple coupled system of one PDE and one ODE.

\begin{matrix} {(V_{1})}^{2} \frac{\partial U_{1}}{\partial t} - x V_{1} {\dot{V}}_{1} \frac{\partial U_{1}}{\partial x} = \frac{\partial^{2} U_{1}}{\partial x^{2}} \\ {\dot{V}}_{1} = V_{1} U_{1} + \frac{\partial U_{1}}{\partial x} + 1 + t, \end{matrix}

for

t \in [10^{- 4}, 0.1 \times 2^{i}], i = 1, 2, \dots, 5, x \in [0, 1]

The left boundary condition at

x = 0

\frac{\partial U_{1}}{\partial x} = - V_{1} \exp t .

The right boundary condition at

x = 1

U_{1} = - V_{1} {\dot{V}}_{1} .

The initial conditions at

t = 10^{- 4}

are defined by the exact solution:

V_{1} = t,   and U_{1} (x, t) = \exp \{t (1 - x)\} - 1.0, x \in [0, 1],

and the coupling point is at

ξ_{1} = 1.0

Open in the MATLAB editor: d03pj_example

function d03pj_example


fprintf('d03pj example results\n\n');

npde   = int64(1);
m      = int64(0);
ts     = 0.0001;
tout   = 0.2;
u      = zeros(22,1);
xbkpts = [0:0.1:1];
npoly  = int64(2);
npts   = int64(21);
ncode  = int64(1);
xi     = [1];
rtol   = [0.0001];
atol   = rtol;
itol   = int64(1);
normt  = 'A';
laopt  = 'F';
algopt = zeros(30,1);
rsave  = zeros(900, 1);
isave  = zeros(24, 1, 'int64');
itask  = int64(1);
itrace = int64(0);
ind   = int64(0);
cwsav = {''; ''; ''; ''; ''; ''; ''; ''; ''; ''};
lwsav = false(100, 1);
iwsav = zeros(505, 1, 'int64');
rwsav = zeros(1100, 1);

t = [0.1:3.1/19:3.2];

for i_t = 1:numel(t)
  tout = t(i_t);
  [ts, u, x, rsave, isave, ind, user, cwsav, lwsav, iwsav, rwsav, ifail] = ...
  d03pj( ...
         npde, m, ts, tout, @pdedef, @bndary, u, xbkpts, ...
         npoly, npts, ncode, @odedef, xi, @uvinit, rtol, atol, itol, ...
         normt, laopt, algopt, rsave, isave, itask, itrace, ind, ...
         cwsav, lwsav, iwsav, rwsav);

  if (i_t==1)
    % with ind==1, x is not returned again
    xs = reshape(x,[7,3]);
  end
  if mod(i_t+4,6)==0
    fprintf('\nThe solution at t = %7.4f is:\n',ts);
    for j = 0:2
      fprintf('%10s%12s','x','u(x,t)');
    end
    fprintf('\n');

    us = reshape(u(1:21),[7,3]);
    for i = 1:7
      for j = 1:3
        fprintf('%12.2f%10.4f',xs(i,j),us(i,j));
      end
      fprintf('\n');
    end
  end
  v(:,i_t) = u(1:(end-1));
end

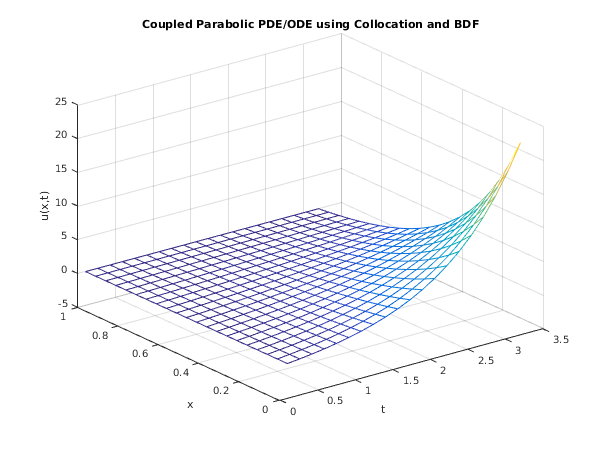
fig1 = figure;
x = reshape(xs,[21,1]);
mesh(t,x,v);
xlabel('t');
ylabel('x');
zlabel('u(x,t)');
title('Coupled Parabolic PDE/ODE using Collocation and BDF');


function [p,q,r,ires,user] = pdedef(npde,t,x,nptl,u,ux,ncode,v,vdot,ires,user)
  p = zeros(npde,npde,nptl);
  q = zeros(npde,nptl);
  r = zeros(npde,nptl);

  p(1,1,:) = v(1)*v(1);
  r(1,:) = ux(1,1:nptl);
  q(1,1:nptl) = -x(1:nptl)'.*ux(1,1:nptl)*(v(1)*vdot(1));

function [beta,gamma,ires,user] = bndary(npde,t,u,ux,ncode,v,vdot,ibnd,...
                                         ires,user)
  beta = zeros(npde,1);
  gamma = zeros(npde,1);
  beta(1) = 1;
  if (ibnd == 0)
    gamma(1) = -v(1)*exp(t);
  else
    gamma(1) = -v(1)*vdot(1);
  end

function [f,ires,user] = odedef(npde,t,ncode,v,vdot,nxi,xi,ucp, ...
                                ucpx,rcp,ucpt,ucptx,ires,user)
  f = zeros(ncode,1);
  if (ires == 1)
    f(1) = vdot(1) - v(1)*ucp(1,1) - ucpx(1,1) - 1 - t;
  elseif (ires == -1)
    f(1) = vdot(1);
  end

function [u,v,user] = uvinit(npde,npts,x,ncode,user)
  u = zeros(npde,npts);
  ts = 1e-4;

  v(1) = ts;
  u = exp(ts*(1-x)) - 1;

d03pj example results


The solution at t =  0.2632 is:
         x      u(x,t)         x      u(x,t)         x      u(x,t)
        0.00    0.3014        0.35    0.1869        0.70    0.0825
        0.05    0.2844        0.40    0.1714        0.75    0.0683
        0.10    0.2676        0.45    0.1561        0.80    0.0543
        0.15    0.2510        0.50    0.1409        0.85    0.0406
        0.20    0.2347        0.55    0.1260        0.90    0.0270
        0.25    0.2185        0.60    0.1113        0.95    0.0135
        0.30    0.2026        0.65    0.0968        1.00    0.0003

The solution at t =  1.2421 is:
         x      u(x,t)         x      u(x,t)         x      u(x,t)
        0.00    2.4634        0.35    1.2421        0.70    0.4514
        0.05    2.2548        0.40    1.1071        0.75    0.3639
        0.10    2.0588        0.45    0.9801        0.80    0.2818
        0.15    1.8746        0.50    0.8609        0.85    0.2045
        0.20    1.7014        0.55    0.7488        0.90    0.1319
        0.25    1.5387        0.60    0.6434        0.95    0.0637
        0.30    1.3858        0.65    0.5444        1.00   -0.0004

The solution at t =  2.2211 is:
         x      u(x,t)         x      u(x,t)         x      u(x,t)
        0.00    8.2169        0.35    3.2347        0.70    0.9449
        0.05    7.2478        0.40    2.7893        0.75    0.7401
        0.10    6.3805        0.45    2.3908        0.80    0.5569
        0.15    5.6045        0.50    2.0341        0.85    0.3929
        0.20    4.9099        0.55    1.7149        0.90    0.2461
        0.25    4.2885        0.60    1.4293        0.95    0.1147
        0.30    3.7323        0.65    1.1736        1.00   -0.0029

The solution at t =  3.2000 is:
         x      u(x,t)         x      u(x,t)         x      u(x,t)
        0.00   23.5336        0.35    6.9983        0.70    1.6052
        0.05   19.9047        0.40    5.8146        0.75    1.2189
        0.10   16.8115        0.45    4.8060        0.80    0.8898
        0.15   14.1765        0.50    3.9466        0.85    0.6092
        0.20   11.9308        0.55    3.2142        0.90    0.3701
        0.25   10.0177        0.60    2.5902        0.95    0.1662
        0.30    8.3873        0.65    2.0584        1.00   -0.0076

PDF version (NAG web site, 64-bit version, 64-bit version)

Chapter Contents

Chapter Introduction

NAG Toolbox