NAG Toolbox: nag_pde_1d_blackscholes_fd (d03nc)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{kopt}$ – int64int32nag_int scalar

Specifies the kind of option to be valued.

$\mathbf{kopt}=1$

A European call option.

$\mathbf{kopt}=2$

An American call option.

$\mathbf{kopt}=3$

A European put option.

$\mathbf{kopt}=4$

An American put option.

Constraint: $\mathbf{kopt}=1$, $2$, $3$ or $4$.

2:     $\mathrm{x}$ – double scalar

The exercise price $X$.

3:     $\mathrm{mesh}$ – string (length ≥ 1)

Indicates the type of finite difference mesh to be used:

$\mathbf{mesh}=\text{'U'}$

Uniform mesh.

$\mathbf{mesh}=\text{'C'}$

Custom mesh supplied by you.

Constraint: $\mathbf{mesh}=\text{'U'}$ or $\text{'C'}$.

4:     $\mathrm{s}\left(\mathbf{ns}\right)$ – double array

If $\mathbf{mesh}=\text{'C'}$, $\mathbf{s}\left(\mathit{i}\right)$ must contain the $\mathit{i}$th stock price in the mesh, for $\mathit{i}=1,2,\dots ,\mathbf{ns}$. These values should be in increasing order, with $\mathbf{s}\left(1\right)=S_{\min }$ and $\mathbf{s}\left(\mathbf{ns}\right)=S_{\max }$.

If $\mathbf{mesh}=\text{'U'}$, $\mathbf{s}\left(1\right)$ must be set to $S_{\min }$ and $\mathbf{s}\left(\mathbf{ns}\right)$ to $S_{\max }$, but $\mathbf{s}\left(2\right),\mathbf{s}\left(3\right),\dots ,\mathbf{s}\left(\mathbf{ns}-1\right)$ need not be initialized, as they will be set internally by the function in order to define a uniform mesh.

Constraints:

• if $\mathbf{mesh}=\text{'C'}$, $\mathbf{s}\left(1\right)\ge 0.0$ and $\mathbf{s}\left(\mathit{i}\right)<\mathbf{s}\left(\mathit{i}+1\right)$, for $\mathit{i}=1,2,\dots ,\mathbf{ns}-1$;
• if $\mathbf{mesh}=\text{'U'}$, $0.0\le \mathbf{s}\left(1\right)<\mathbf{s}\left(\mathbf{ns}\right)$.

5:     $\mathrm{t}\left(\mathbf{nt}\right)$ – double array

If $\mathbf{mesh}=\text{'C'}$ then $\mathbf{t}\left(\mathit{j}\right)$ must contain the $\mathit{j}$th time in the mesh, for $\mathit{j}=1,2,\dots ,\mathbf{nt}$. These values should be in increasing order, with $\mathbf{t}\left(1\right)=t_{\min }$ and $\mathbf{t}\left(\mathbf{nt}\right)=t_{\max }$.

If $\mathbf{mesh}=\text{'U'}$ then $\mathbf{t}\left(1\right)$ must be set to $t_{\min }$ and $\mathbf{t}\left(\mathbf{nt}\right)$ to $t_{\max }$, but $\mathbf{t}\left(2\right),\mathbf{t}\left(3\right),\dots ,\mathbf{t}\left(\mathbf{nt}-1\right)$ need not be initialized, as they will be set internally by the function in order to define a uniform mesh.

Constraints:

• if $\mathbf{mesh}=\text{'C'}$, $\mathbf{t}\left(1\right)\ge 0.0$ and $\mathbf{t}\left(\mathit{j}\right)<\mathbf{t}\left(\mathit{j}+1\right)$, for $\mathit{j}=1,2,\dots ,\mathbf{nt}-1$;
• if $\mathbf{mesh}=\text{'U'}$, $0.0\le \mathbf{t}\left(1\right)<\mathbf{t}\left(\mathbf{nt}\right)$.

6:     $\mathrm{tdpar}\left(3\right)$ – logical array

Specifies whether or not various arguments are time-dependent. More precisely, $r$ is time-dependent if $\mathbf{tdpar}\left(1\right)=\mathit{true}$ and constant otherwise. Similarly, $\mathbf{tdpar}\left(2\right)$ specifies whether $q$ is time-dependent and $\mathbf{tdpar}\left(3\right)$ specifies whether $\sigma$ is time-dependent.

7:     $\mathrm{r}\left(:\right)$ – double array

The dimension of the array r must be at least $\mathbf{nt}$ if $\mathbf{tdpar}\left(1\right)=\mathit{true}$, and at least $1$ otherwise

If $\mathbf{tdpar}\left(1\right)=\mathit{true}$ then $\mathbf{r}\left(\mathit{j}\right)$ must contain the value of the risk-free interest rate $r\left(t\right)$ at the $\mathit{j}$th time in the mesh, for $\mathit{j}=1,2,\dots ,\mathbf{nt}$.

If $\mathbf{tdpar}\left(1\right)=\mathit{false}$ then $\mathbf{r}\left(1\right)$ must contain the constant value of the risk-free interest rate $r$. The remaining elements need not be set.

8:     $\mathrm{q}\left(:\right)$ – double array

The dimension of the array q must be at least $\mathbf{nt}$ if $\mathbf{tdpar}\left(2\right)=\mathit{true}$, and at least $1$ otherwise

If $\mathbf{tdpar}\left(2\right)=\mathit{true}$ then $\mathbf{q}\left(\mathit{j}\right)$ must contain the value of the continuous dividend $q\left(t\right)$ at the $\mathit{j}$th time in the mesh, for $\mathit{j}=1,2,\dots ,\mathbf{nt}$.

If $\mathbf{tdpar}\left(2\right)=\mathit{false}$ then $\mathbf{q}\left(1\right)$ must contain the constant value of the continuous dividend $q$. The remaining elements need not be set.

9:     $\mathrm{sigma}\left(:\right)$ – double array

The dimension of the array sigma must be at least $\mathbf{nt}$ if $\mathbf{tdpar}\left(3\right)=\mathit{true}$, and at least $1$ otherwise

If $\mathbf{tdpar}\left(3\right)=\mathit{true}$ then $\mathbf{sigma}\left(\mathit{j}\right)$ must contain the value of the volatility $\sigma \left(t\right)$ at the $\mathit{j}$th time in the mesh, for $\mathit{j}=1,2,\dots ,\mathbf{nt}$.

If $\mathbf{tdpar}\left(3\right)=\mathit{false}$ then $\mathbf{sigma}\left(1\right)$ must contain the constant value of the volatility $\sigma$. The remaining elements need not be set.

10:   $\mathrm{ntkeep}$ – int64int32nag_int scalar

The number of solutions to be stored in the time direction. The function calculates the solution backwards from $\mathbf{t}\left(\mathbf{nt}\right)$ to $\mathbf{t}\left(1\right)$ at all times in the mesh. These time solutions and the corresponding Greeks will be stored at times $\mathbf{t}\left(\mathit{i}\right)$, for $\mathit{i}=1,2,\dots ,\mathbf{ntkeep}$, in the arrays f, theta, delta, gamma, lambda and rho. Other time solutions will be discarded. To store all time solutions set $\mathbf{ntkeep}=\mathbf{nt}$.

Constraint: $1\le \mathbf{ntkeep}\le \mathbf{nt}$.

Optional Input Parameters

1:     $\mathrm{ns}$ – int64int32nag_int scalar

Default: the dimension of the array s.

The number of stock prices to be used in the finite difference mesh.

Constraint: $\mathbf{ns}\ge 2$.

2:     $\mathrm{nt}$ – int64int32nag_int scalar

Default: the dimension of the array t.

The number of time-steps to be used in the finite difference method.

Constraint: $\mathbf{nt}\ge 2$.

3:     $\mathrm{alpha}$ – double scalar

Default: $0.55$

The value of $\lambda$ to be used in the time-stepping scheme. Typical values include:

$\mathbf{alpha}=0.0$

Explicit forward Euler scheme.

$\mathbf{alpha}=0.5$

Implicit Crank–Nicolson scheme.

$\mathbf{alpha}=1.0$

Implicit backward Euler scheme.

The value $0.5$ gives second-order accuracy in time. Values greater than $0.5$ give unconditional stability. Since $0.5$ is at the limit of unconditional stability this value does not damp oscillations.

Constraint: $0.0\le \mathbf{alpha}\le 1.0$.

Output Parameters

1:     $\mathrm{s}\left(\mathbf{ns}\right)$ – double array

If $\mathbf{mesh}=\text{'U'}$, the elements of s define a uniform mesh over $\left[S_{\min },S_{\max }\right]$.

If $\mathbf{mesh}=\text{'C'}$, the elements of s are unchanged.

2:     $\mathrm{t}\left(\mathbf{nt}\right)$ – double array

If $\mathbf{mesh}=\text{'U'}$, the elements of t define a uniform mesh over $\left[t_{\min },t_{\max }\right]$.

If $\mathbf{mesh}=\text{'C'}$, the elements of t are unchanged.

3:     $\mathrm{f}\left(\mathit{ldf},\mathbf{ntkeep}\right)$ – double array

$\mathbf{f}\left(\mathit{i},\mathit{j}\right)$, for $\mathit{i}=1,2,\dots ,\mathbf{ns}$ and $\mathit{j}=1,2,\dots ,\mathbf{ntkeep}$, contains the value $f$ of the option at the $\mathit{i}$th mesh point $\mathbf{s}\left(\mathit{i}\right)$ at time $\mathbf{t}\left(\mathit{j}\right)$.

4:     $\mathrm{theta}\left(\mathit{ldf},\mathbf{ntkeep}\right)$ – double array

5:     $\mathrm{delta}\left(\mathit{ldf},\mathbf{ntkeep}\right)$ – double array

6:     $\mathrm{gamma}\left(\mathit{ldf},\mathbf{ntkeep}\right)$ – double array

7:     $\mathrm{lambda}\left(\mathit{ldf},\mathbf{ntkeep}\right)$ – double array

8:     $\mathrm{rho}\left(\mathit{ldf},\mathbf{ntkeep}\right)$ – double array

The values of various Greeks at the $i$th mesh point $\mathbf{s}\left(i\right)$ at time $\mathbf{t}\left(j\right)$, as follows:

$$\begin{array}{lll}\mathbf{theta}\left(i,j\right)=\frac{\partial f}{\partial t}\text{,}& \mathbf{delta}\left(i,j\right)=\frac{\partial f}{\partial S}\text{,}& \mathbf{gamma}\left(i,j\right)=\frac{{\partial }^{2}f}{\partial S^2}\text{,}\\ \\ \mathbf{lambda}\left(i,j\right)=\frac{\partial f}{\partial \sigma }\text{,}& \mathbf{rho}\left(i,j\right)=\frac{\partial f}{\partial r}\text{.}\end{array}$$

9:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

   $\mathbf{ifail}=1$

On entry,	$\mathbf{kopt}<1$,
or	$\mathbf{kopt}>4$,
or	$\mathbf{mesh}\ne \text{'U'}$ or $\text{'C'}$,
or	$\mathbf{ns}<2$,
or	$\mathbf{nt}<2$,
or	$\mathbf{s}\left(1\right)<0.0$,
or	$\mathbf{t}\left(1\right)<0.0$,
or	$\mathbf{alpha}<0.0$,
or	$\mathbf{alpha}>1.0$,
or	$\mathbf{ntkeep}<1$,
or	$\mathbf{ntkeep}>\mathbf{nt}$,
or	$\mathit{ldf}<\mathbf{ns}$.

   $\mathbf{ifail}=2$

$\mathbf{mesh}=\text{'U'}$ and the constraints:

• $\mathbf{s}\left(1\right)<\mathbf{s}\left(\mathbf{ns}\right)$,
• $\mathbf{t}\left(1\right)<\mathbf{t}\left(\mathbf{nt}\right)$

are violated. Thus the end points of the uniform mesh are not in order.

   $\mathbf{ifail}=3$

$\mathbf{mesh}=\text{'C'}$ and the constraints:

• $\mathbf{s}\left(\mathit{i}\right)<\mathbf{s}\left(\mathit{i}+1\right)$, for $\mathit{i}=1,2,\dots ,\mathbf{ns}-1$,
• $\mathbf{t}\left(\mathit{i}\right)<\mathbf{t}\left(\mathit{i}+1\right)$, for $\mathit{i}=1,2,\dots ,\mathbf{nt}-1$ 

are violated. Thus the mesh points are not in order.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Timing

Algorithmic Details

Example

Open in the MATLAB editor: d03nc_example

function d03nc_example


fprintf('d03nc example results\n\n');

% American put option with exercise price 50
kopt = int64(4);
x    = 50;

% Use uniform mesh of 21 stock prices [0:100] and 11 time-steps [0:0.416667]
mesh = 'U';
n    = 21;
nt   = 11;
s    = zeros(n,1);
s(n) = 100;
t    = zeros(nt,1);
t(nt) = 0.4166667;

% Parameters are not time-dependent
tdpar = [false; false; false];
r     = [0.1];
q     = [0];
sigma = [0.4];

% Keep 4 solutions in time and use backward Euler scheme.
ntkeep = int64(4);
alpha  = 1;

[s, t, f, theta, delta, gamma, lambda, rho, ifail] = ...
    d03nc(...
          kopt, x, mesh, s, t, tdpar, r, q, sigma, ntkeep,'alpha',alpha);

disp('         Option Values');
disp('  Stock Price  |   Time to Maturity (months)');
fprintf('%16s','|');
fprintf('%12.1f',12*(t(nt)-t(1:ntkeep))); 
fprintf('\n');
for i = 1:n
  fprintf('%12.0f%4s', s(i), '|');
  fprintf(' %12.5f', f(i,:));
  fprintf('\n');
end

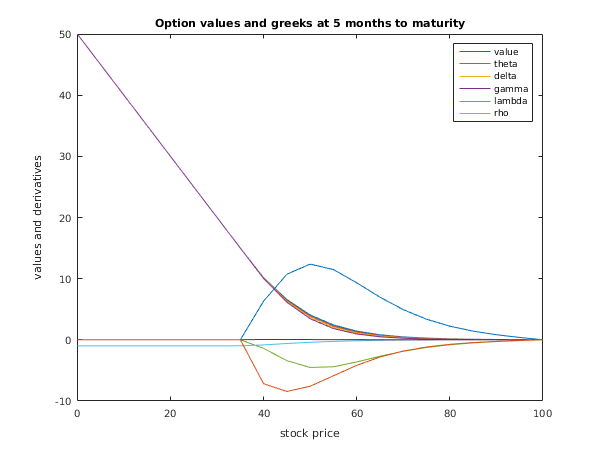
fig1 = figure;
plot(s,f,s,theta(:,1),s,delta(:,1),s,gamma(:,1),s,...
     lambda(:,1),s,rho(:,1));
legend('value','theta','delta','gamma','lambda','rho');
title('Option values and greeks at 5 months to maturity');
xlabel('stock price');
ylabel('values and derivatives');

d03nc example results

         Option Values
  Stock Price  |   Time to Maturity (months)
               |         5.0         4.5         4.0         3.5
           0   |     50.00000     50.00000     50.00000     50.00000
           5   |     45.00000     45.00000     45.00000     45.00000
          10   |     40.00000     40.00000     40.00000     40.00000
          15   |     35.00000     35.00000     35.00000     35.00000
          20   |     30.00000     30.00000     30.00000     30.00000
          25   |     25.00000     25.00000     25.00000     25.00000
          30   |     20.00000     20.00000     20.00000     20.00000
          35   |     15.00000     15.00000     15.00000     15.00000
          40   |     10.15432     10.09580     10.04640     10.01169
          45   |      6.58481      6.44237      6.29161      6.13058
          50   |      4.06719      3.87850      3.67292      3.44630
          55   |      2.42637      2.24235      2.04536      1.83361
          60   |      1.41742      1.26619      1.10958      0.94813
          65   |      0.81951      0.70724      0.59532      0.48515
          70   |      0.47241      0.39411      0.31904      0.24845
          75   |      0.27257      0.22016      0.17174      0.12815
          80   |      0.15725      0.12328      0.09294      0.06668
          85   |      0.08966      0.06848      0.05010      0.03473
          90   |      0.04845      0.03625      0.02590      0.01747
          95   |      0.02110      0.01558      0.01097      0.00727
         100   |      0.00000      0.00000      0.00000      0.00000