hide long namesshow long names
hide short namesshow short names
Integer type:  int32  int64  nag_int  show int32  show int32  show int64  show int64  show nag_int  show nag_int
PDF version (NAG web site, 64-bit version, 64-bit version)
Chapter Contents
Chapter Introduction
NAG Toolbox

NAG Toolbox: nag_ode_bvp_coll_nlin_interp (d02ty)

▸▿ Contents

    1  Purpose
    2  Syntax
    3  Description
    4  References
▸▿ 5  Parameters
    6  Error Indicators and Warnings
    7  Accuracy
    8  Further Comments
    9  Example

Purpose

nag_ode_bvp_coll_nlin_interp (d02ty) interpolates on the solution of a general two-point boundary value problem computed by nag_ode_bvp_coll_nlin_solve (d02tl).

Syntax

[y, rcomm, ifail] = d02ty(x, neq, mmax, rcomm, icomm)
[y, rcomm, ifail] = nag_ode_bvp_coll_nlin_interp(x, neq, mmax, rcomm, icomm)

Description

nag_ode_bvp_coll_nlin_interp (d02ty) and its associated functions (nag_ode_bvp_coll_nlin_solve (d02tl), nag_ode_bvp_coll_nlin_setup (d02tv), nag_ode_bvp_coll_nlin_contin (d02tx) and nag_ode_bvp_coll_nlin_diag (d02tz)) solve the two-point boundary value problem for a nonlinear mixed order system of ordinary differential equations
y1m1 x = f1 x,y1,y11,…,y1m1-1,y2,…,ynmn-1 y2m2 x = f2 x,y1,y11,…,y1m1-1,y2,…,ynmn-1 ⋮ ynmn x = fn x,y1,y11,…,y1m1-1,y2,…,ynmn-1  
over an interval a,b subject to p (>0) nonlinear boundary conditions at a and q (>0) nonlinear boundary conditions at b, where p+q = ∑ i=1 n mi . Note that yi m x is the mth derivative of the ith solution component. Hence yi 0 x=yix. The left boundary conditions at a are defined as
gizya=0,  i=1,2,…,p,  
and the right boundary conditions at b as
g-jzyb=0,  j=1,2,…,q,  
where y=y1,y2,…,yn and
zyx = y1x, y11 x ,…, y1m1-1 x ,y2x,…, ynmn-1 x .  
First, nag_ode_bvp_coll_nlin_setup (d02tv) must be called to specify the initial mesh, error requirements and other details. Then, nag_ode_bvp_coll_nlin_solve (d02tl) can be used to solve the boundary value problem. After successful computation, nag_ode_bvp_coll_nlin_diag (d02tz) can be used to ascertain details about the final mesh and other details of the solution procedure, and nag_ode_bvp_coll_nlin_interp (d02ty) can be used to compute the approximate solution anywhere on the interval a,b using interpolation.
The functions are based on modified versions of the codes COLSYS and COLNEW (see Ascher et al. (1979) and Ascher and Bader (1987)). A comprehensive treatment of the numerical solution of boundary value problems can be found in Ascher et al. (1988) and Keller (1992).

References

Ascher U M and Bader G (1987) A new basis implementation for a mixed order boundary value ODE solver SIAM J. Sci. Stat. Comput. 8 483–500
Ascher U M, Christiansen J and Russell R D (1979) A collocation solver for mixed order systems of boundary value problems Math. Comput. 33 659–679
Ascher U M, Mattheij R M M and Russell R D (1988) Numerical Solution of Boundary Value Problems for Ordinary Differential Equations Prentice–Hall
Grossman C (1992) Enclosures of the solution of the Thomas–Fermi equation by monotone discretization J. Comput. Phys. 98 26–32
Keller H B (1992) Numerical Methods for Two-point Boundary-value Problems Dover, New York

Parameters

Compulsory Input Parameters

1:     x – double scalar
x, the independent variable.
Constraint: a≤x≤b, i.e., not outside the range of the original mesh specified in the initialization call to nag_ode_bvp_coll_nlin_setup (d02tv).
2:     neq – int64int32nag_int scalar
The number of differential equations.
Constraint: neq must be the same value as supplied to nag_ode_bvp_coll_nlin_setup (d02tv).
3:     mmax – int64int32nag_int scalar
The maximal order of the differential equations, maxmi, for i=1,2,…,neq.
Constraint: mmax must contain the maximum value of the components of the argument m as supplied to nag_ode_bvp_coll_nlin_setup (d02tv).
4:     rcomm* – double array
Note: the dimension of this array is dictated by the requirements of associated functions that must have been previously called. This array must be the same array passed as argument rcomm in the previous call to nag_ode_bvp_coll_nlin_solve (d02tl).
This must be the same array as supplied to nag_ode_bvp_coll_nlin_solve (d02tl) and must remain unchanged between calls.
5:     icomm* – int64int32nag_int array
Note: the dimension of this array is dictated by the requirements of associated functions that must have been previously called. This array must be the same array passed as argument icomm in the previous call to nag_ode_bvp_coll_nlin_solve (d02tl).
This must be the same array as supplied to nag_ode_bvp_coll_nlin_solve (d02tl) and must remain unchanged between calls.

Optional Input Parameters

None.

Output Parameters

1:     yneqmmax – double array
yij contains an approximation to yi j x, for i=1,2,…,neq and j=0,1,…,mi-1. The remaining elements of y (where mi<mmax) are initialized to 0.0.
2:     rcomm* – double array
Note: the dimension of this array is dictated by the requirements of associated functions that must have been previously called. This array must be the same array passed as argument rcomm in the previous call to nag_ode_bvp_coll_nlin_solve (d02tl).
Contains information about the solution for use on subsequent calls to associated functions.
3:     ifail – int64int32nag_int scalar
ifail=0 unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Note: nag_ode_bvp_coll_nlin_interp (d02ty) may return useful information for one or more of the following detected errors or warnings.
Errors or warnings detected by the function:
   ifail=1
Constraint: mmax=max⁡mi.
Constraint: neq=neq in nag_ode_bvp_coll_nlin_setup (d02tv).
Constraint: x≤_.
The solver function did not produce any results suitable for interpolation.
The solver function does not appear to have been called.
x is too small.
   ifail=2
The solver function did not converge to a suitable solution.
A converged intermediate solution has been used.
Interpolated values should be treated with caution.
The solver function did not satisfy the error requirements.
Interpolated values should be treated with caution.
   ifail=-99
An unexpected error has been triggered by this routine. Please contact NAG.
   ifail=-399
Your licence key may have expired or may not have been installed correctly.
   ifail=-999
Dynamic memory allocation failed.

Accuracy

If nag_ode_bvp_coll_nlin_interp (d02ty) returns the value ifail=0, the computed values of the solution components yi should be of similar accuracy to that specified by the argument tols of nag_ode_bvp_coll_nlin_setup (d02tv). Note that during the solution process the error in the derivatives yij, for j=1,2,…,mi-1, has not been controlled and that the derivative values returned by nag_ode_bvp_coll_nlin_interp (d02ty) are computed via differentiation of the piecewise polynomial approximation to yi. See also Further Comments.

Further Comments

If nag_ode_bvp_coll_nlin_interp (d02ty) returns the value ifail=2 in this function and ifail=5 in nag_ode_bvp_coll_nlin_solve (d02tl), then the accuracy of the interpolated values may be proportional to the quantity ermx as returned by nag_ode_bvp_coll_nlin_diag (d02tz).
If nag_ode_bvp_coll_nlin_solve (d02tl) returned a value for ifail other than ifail=0, then nothing can be said regarding either the quality or accuracy of the values computed by nag_ode_bvp_coll_nlin_interp (d02ty).

Example

The following example is used to illustrate that a system with singular coefficients can be treated without modification of the system definition. See also nag_ode_bvp_coll_nlin_solve (d02tl), nag_ode_bvp_coll_nlin_setup (d02tv), nag_ode_bvp_coll_nlin_contin (d02tx) and nag_ode_bvp_coll_nlin_diag (d02tz), for the illustration of other facilities.
Consider the Thomas–Fermi equation used in the investigation of potentials and charge densities of ionized atoms. See Grossman (1992), for example, and the references therein. The equation is
y′′=x-1/2y3/2  
with boundary conditions
y0= 1,   ya= 0,   a> 0.  
The coefficient x-1/2 implies a singularity at the left-hand boundary x=0.
We use the initial approximation yx=1-x/a, which satisfies the boundary conditions, on a uniform mesh of six points. For illustration we choose a=1, as in Grossman (1992). Note that in ffun and fjac (see nag_ode_bvp_coll_nlin_solve (d02tl)) we have taken the precaution of setting the function value and Jacobian value to 0.0 in case a value of y becomes negative, although starting from our initial solution profile this proves unnecessary during the solution phase. Of course the true solution yx is positive for all x<a.

Open in the MATLAB editor: d02ty_example

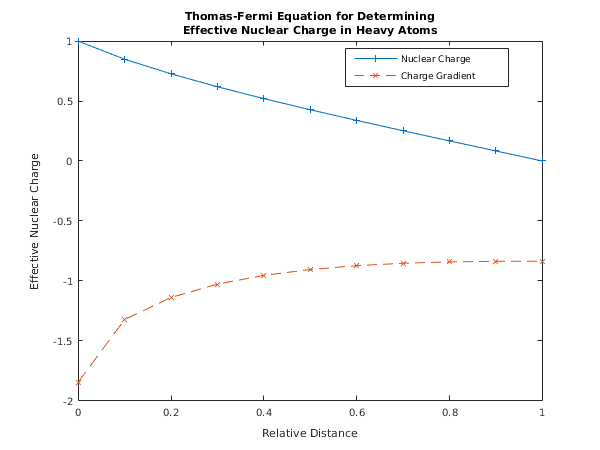
function d02ty_example


fprintf('d02ty example results\n\n');

global a; % For communication with local functions

% Initialize variables and arrays.
neq  = int64(1);
nlbc = int64(1);
nrbc = int64(1);
ncol = int64(4);
mmax = int64(2);
m    = int64([2]);
tols = [1.0e-05];

% Set values for problem-specific physical parameters.
a = 1.0;

% Set up the mesh.
nmesh  = int64(6);
mxmesh = int64(100);
ipmesh = zeros(mxmesh, 1, 'int64');
mesh   = zeros(mxmesh, 1);

% Set initial mesh with constant spacing.
dx = a/double(nmesh-1);
mesh(1:nmesh) = [0:dx:a];

% Specify mesh end points as fixed.
ipmesh(1)         = 1;
ipmesh(2:nmesh-1) = 2;
ipmesh(nmesh)     = 1;

% d02tv is a setup routine to be called prior to d02tk.
[work, iwork, ifail] = d02tv(...
                              m, nlbc, nrbc, ncol, tols, nmesh, mesh, ipmesh);
fprintf('\n Tolerance = %8.1e  A = %8.2f\n\n', tols(1), a);

% Call d02tk to solve BVP for this set of parameters.
[work, iwork, ifail] = d02tk(...
                             @ffun, @fjac, @gafun, @gbfun, @gajac, @gbjac,...
                             @guess, work, iwork);

% Call d02tz to extract mesh from solution.
[nmesh, mesh, ipmesh, ermx, iermx, ijermx, ifail] = ...
d02tz( ...
       mxmesh, work, iwork);

% Output mesh results.
fprintf(' Used a mesh of %d points\n', nmesh);
fprintf([' Maximum error = %10.2e in interval %d for component %d\n\n', ...
         ' Mesh points:\n'], ermx, iermx, ijermx);
for imesh = 1:nmesh
  fprintf( '%4d(%d) %6.4f', imesh, ipmesh(imesh), mesh(imesh));
  if mod(imesh, 4) == 0
    fprintf('\n');
  end
end

% Output solution, and store it for plotting.
xarray = zeros(nmesh, 1);
yarray = zeros(nmesh, 2);
fprintf('\n\n Computed solution\n');
fprintf('       x     solution   derivative\n');
for imesh = 1:nmesh
  % Call d02ty to perform interpolation on the solution.
  xx = mesh(imesh);
  [y, work, ifail] = d02ty(...
                           xx, neq, mmax, work, iwork);
  fprintf(' %8.2f %10.5f %10.5f\n', xx, y(1,1), y(1,2));
  xarray(imesh) = xx;
  yarray(imesh, :) = y(1, :);
end
% Plot results.
fig1 = figure;
display_plot(xarray, yarray);


function [f] = ffun(x, y, neq, m)
  % Evaluate derivative functions (rhs of system of ODEs).

  f = zeros(neq, 1);
  if y(1,1) < 0
    f(1,1) = 0;
    fprintf(' In ffun\n');
  else
    f(1,1) = y(1,1)^1.5/sqrt(x);
  end

function [dfdy] = fjac(x, y, neq, m)
  % Evaluate Jacobians (partial derivatives of f).

  dfdy = zeros(neq, neq, 2);
  if y(1,1) < 0
    dfdy(1,1,1) = 0;
    fprintf(' In fjac\n');
  else
    dfdy(1,1,1) = 1.5*sqrt(y(1,1))/sqrt(x);
  end

function [ga] = gafun(ya, neq, m, nlbc)
  % Evaluate boundary conditions at left-hand end of range.

  ga = zeros(nlbc, 1);
  ga(1,1) = ya(1,1) - 1;

function [dgady] = gajac(ya, neq, m, nlbc)
  % Evaluate Jacobians (partial derivatives of ga).

  dgady = zeros(nlbc, neq, 2);
  dgady(1,1,1) = 1;

function [gb] = gbfun(yb, neq, m, nrbc)
  % Evaluate boundary conditions at right-hand end of range.

  gb = zeros(nrbc, 1);
  gb(1,1) = yb(1,1);

function [dgbdy] = gbjac(yb, neq, m, nrbc)
  % Evaluate Jacobians (partial derivatives of gb).

  dgbdy = zeros(nrbc, neq, 2);
  dgbdy(1,1,1) = 1;

function [y, dym] = guess(x, neq, m)
  % Evaluate initial approximations to solution components and derivatives.

  global a
  y = zeros(neq, 2);
  dym = zeros(neq, 1);
  y(1,1) =  1 - x/a;
  y(1,2) = -1/a;

  dym(1) = 0;

function display_plot(x, y)
  % Plot both curves.
  [hline] = plot(x, y(:,1), x, y(:,2));
  % Add title.
  title({['Thomas-Fermi Equation for Determining'],...
         ['Effective Nuclear Charge in Heavy Atoms']});
  % Label the axes.
  xlabel('Relative Distance');
  ylabel('Effective Nuclear Charge');
  % Add a legend.
  legend('Nuclear Charge','Charge Gradient','Location','Best')
  % Set some features of the three lines.
  set(hline(1), 'Linewidth', 0.25, 'Marker', '+', 'LineStyle', '-');
  set(hline(2), 'Linewidth', 0.25, 'Marker', 'x', 'LineStyle', '--');

d02ty example results


 Tolerance =  1.0e-05  A =     1.00

 Used a mesh of 11 points
 Maximum error =   3.09e-06 in interval 1 for component 1

 Mesh points:
   1(1) 0.0000   2(3) 0.1000   3(2) 0.2000   4(3) 0.3000
   5(2) 0.4000   6(3) 0.5000   7(2) 0.6000   8(3) 0.7000
   9(2) 0.8000  10(3) 0.9000  11(1) 1.0000

 Computed solution
       x     solution   derivative
     0.00    1.00000   -1.84496
     0.10    0.84944   -1.32330
     0.20    0.72721   -1.13911
     0.30    0.61927   -1.02776
     0.40    0.52040   -0.95468
     0.50    0.42754   -0.90583
     0.60    0.33867   -0.87372
     0.70    0.25239   -0.85369
     0.80    0.16764   -0.84248
     0.90    0.08368   -0.83756
     1.00    0.00000   -0.83655
d02ty_fig1.png
PDF version (NAG web site, 64-bit version, 64-bit version)
Chapter Contents
Chapter Introduction
NAG Toolbox
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015