| – | cluster the mesh points where sharp changes in behaviour are expected; |
| – | maintain fixed points in the mesh using the argument ipmesh to ensure that the remeshing process does not inadvertently remove mesh points from areas of known interest. |
Open in the MATLAB editor: d02tx_example
function d02tx_example fprintf('d02tx example results\n\n'); global en s el; % For communication with local functions % Initialize variables and arrays. neq = int64(2); nlbc = int64(3); nrbc = int64(2); ncol = int64(6); mmax = int64(3); m = int64([3; 2]); tols = [0.00001; 0.00001]; % Set values for problem-specific physical parameters. el = 60; s = 0.24; en = 0.2; % Set up the mesh. nmesh = int64(21); mxmesh = int64(250); mesh = zeros(mxmesh,1); ipmesh = zeros(mxmesh,1,'int64'); % Set initial mesh with constant spacing. dx = 1/double(nmesh-1); mesh(1:nmesh) = [0:dx:1]; % Specify mesh end points as fixed. ipmesh(1) = 1; ipmesh(2:nmesh-1) = 2; ipmesh(nmesh) = 1; % Prepare to store results for plotting. xarray = zeros(1,1); yarray1 = zeros(1,1); yarray2 = zeros(1,1); % d02tv is a setup routine to be called prior to d02tk. [work, iwork, ifail] = d02tv(... m, nlbc, nrbc, ncol, tols, nmesh, mesh, ipmesh); ncont = 3; % We run through the calculation three times with different parameter sets. for jcont = 1:ncont fprintf('\n Tolerance = %8.1e, L = %8.3f, S = %6.4f\n\n', tols(1), el, s); % Call d02tk to solve BVP for this set of parameters. [work, iwork, ifail] = d02tk(... @ffun, @fjac, @gafun, @gbfun, @gajac, ... @gbjac, @guess, work, iwork); % Call d02tz to extract mesh from solution. [nmesh, mesh, ipmesh, ermx, iermx, ijermx, ifail] = ... d02tz( ... mxmesh, work, iwork); % Output mesh results. fprintf(' Used a mesh of %d points\n', nmesh); fprintf(' Maximum error = %10.2e in interval %d for component %d\n\n',... ermx, iermx, ijermx); % Output solution, and store it for plotting. fprintf(' Solution on original interval:\n'); fprintf(' x f g\n'); for i=1:16 xx = double(i-1)*2/el; % Call d02ty to perform interpolation on the solution. [y, work, ifail] = d02ty(... xx, neq, mmax, work, iwork); fprintf(' %6.2f %8.4f %8.4f\n', xx*el, y(1,1), y(2,1)); xarray(i) = xx*el; yarray1(i) = y(1,1); yarray2(i) = y(2,1); end for i=1:10 xx = (30+(el-30)*double(i)/10)/el; [y, work, ifail] = d02ty(... xx, neq, mmax, work, iwork); fprintf(' %6.2f %8.4f %8.4f\n', xx*el, y(1,1), y(2,1)); xarray(i+16) = xx*el; yarray1(i+16) = y(1,1); yarray2(i+16) = y(2,1); end % Plot results for this parameter set. if (jcont==1) fig1 = figure; elseif (jcont==2) fig2 = figure; else fig3 = figure; end display_plot(xarray, yarray1, yarray2, el, s) % Select mesh for next calculation. if jcont < ncont el = 2*el; s = 0.6*s; nmesh = (nmesh+1)/2; % d02tx allows the current solution to be used as an initial % approximation to the solution of a related problem. [work, iwork, ifail] = d02tx(... nmesh, mesh, ipmesh, work, iwork); end end function [f] = ffun(x, y, neq, m) % Evaluate derivative functions (rhs of system of ODEs). global en s el f = zeros(neq, 1); f(1) = el^3*(1-y(2,1)^2) + el^2*s*y(1,2) - ... el*(0.5*(3-en)*y(1,1)*y(1,3) + en*y(1,2)^2); f(2) = el^2*s*(y(2,1)-1) - ... el*(0.5*(3-en)*y(1,1)*y(2,2) + (en-1)*y(1,2)*y(2,1)); function [dfdy] = fjac(x, y, neq, m) % Evaluate Jacobians (partial derivatives of f). global en s el dfdy = zeros(neq, neq, 3); dfdy(1,2,1) = -2*el^3*y(2,1); dfdy(1,1,1) = -el*0.5*(3-en)*y(1,3); dfdy(1,1,2) = el^2*s - el*2*en*y(1,2); dfdy(1,1,3) = -el*0.5*(3-en)*y(1,1); dfdy(2,2,1) = el^2*s - el*(en-1)*y(1,2); dfdy(2,2,2) = -el*0.5*(3-en)*y(1,1); dfdy(2,1,1) = -el*0.5*(3-en)*y(2,2); dfdy(2,1,2) = -el*(en-1)*y(2,1); function [ga] = gafun(ya, neq, m, nlbc) % Evaluate boundary conditions at left-hand end of range. global en s el ga = zeros(nlbc, 1); ga(1) = ya(1,1); ga(2) = ya(1,2); ga(3) = ya(2,1); function [dgady] = gajac(ya, neq, m, nlbc) % Evaluate Jacobians (partial derivatives of ga). global en s el dgady = zeros(nlbc, neq, 3); dgady(1,1,1) = 1; dgady(2,1,2) = 1; dgady(3,2,1) = 1; function [gb] = gbfun(yb, neq, m, nrbc) % Evaluate boundary conditions at right-hand end of range. global en s el gb = zeros(nrbc, 1); gb(1) = yb(1,2); gb(2) = yb(2,1) - 1; function [dgbdy] = gbjac(yb, neq, m, nrbc) % Evaluate Jacobians (partial derivatives of gb). global en s el dgbdy = zeros(nrbc, neq, 3); dgbdy(1,1,2) = 1; dgbdy(2,2,1) = 1; function [y, dym] = guess(x, neq, m) % Evaluate initial approximations to solution components and derivatives. global en s el y = zeros(neq, 3); dym = zeros(neq, 1); ex = x*el; expmx = exp(-ex); y(1,1) = -ex^2*expmx; y(1,2) = (-2*ex+ex^2)*expmx; y(1,3) = (-2+4*ex-ex^2)*expmx; y(2,1) = 1 - expmx; y(2,2) = expmx; dym(1) = (6-6*ex+ex^2)*expmx; dym(2) = -expmx; function display_plot(xarray,yarray1,yarray2,el,s) % Formatting for title and axis labels. % Plot the results. plot(xarray, yarray1, '-+', xarray, yarray2, '--x'); % Add title. title({['Swirling Flow over Disc in Axial Magnetic Field '], ... ['with L = ',num2str(el), ' and s = ',num2str(s)]}) % Label the axes. xlabel('Radial Distance from Magnetic Field'); ylabel('Velocities'); % Add a legend. legend('axial velocity','tangential velocity','Location','Best')
d02tx example results
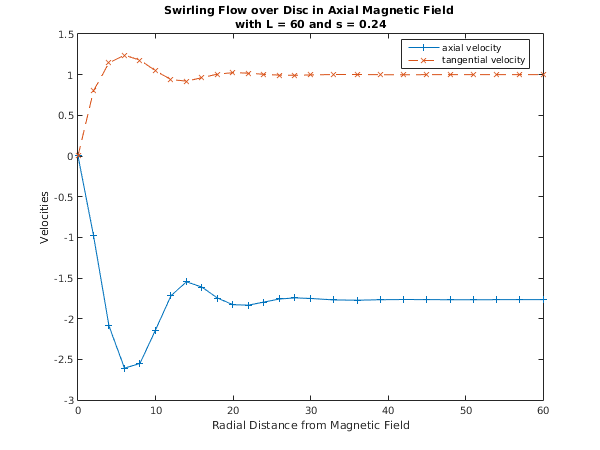
Tolerance = 1.0e-05, L = 60.000, S = 0.2400
Used a mesh of 21 points
Maximum error = 2.66e-08 in interval 7 for component 1
Solution on original interval:
x f g
0.00 0.0000 0.0000
2.00 -0.9769 0.8011
4.00 -2.0900 1.1459
6.00 -2.6093 1.2389
8.00 -2.5498 1.1794
10.00 -2.1397 1.0478
12.00 -1.7176 0.9395
14.00 -1.5465 0.9206
16.00 -1.6127 0.9630
18.00 -1.7466 1.0068
20.00 -1.8286 1.0244
22.00 -1.8338 1.0185
24.00 -1.7956 1.0041
26.00 -1.7582 0.9940
28.00 -1.7445 0.9926
30.00 -1.7515 0.9965
33.00 -1.7695 1.0019
36.00 -1.7730 1.0018
39.00 -1.7673 0.9998
42.00 -1.7645 0.9993
45.00 -1.7659 0.9999
48.00 -1.7672 1.0002
51.00 -1.7671 1.0001
54.00 -1.7666 0.9999
57.00 -1.7665 0.9999
60.00 -1.7666 1.0000
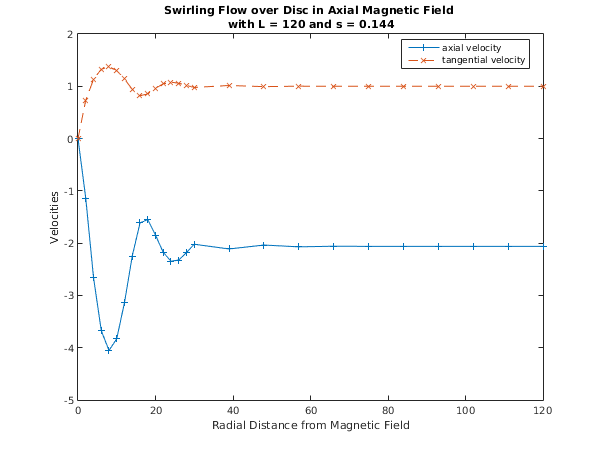
Tolerance = 1.0e-05, L = 120.000, S = 0.1440
Used a mesh of 21 points
Maximum error = 6.88e-06 in interval 7 for component 2
Solution on original interval:
x f g
0.00 0.0000 0.0000
2.00 -1.1406 0.7317
4.00 -2.6531 1.1315
6.00 -3.6721 1.3250
8.00 -4.0539 1.3707
10.00 -3.8285 1.3003
12.00 -3.1339 1.1407
14.00 -2.2469 0.9424
16.00 -1.6146 0.8201
18.00 -1.5472 0.8549
20.00 -1.8483 0.9623
22.00 -2.1761 1.0471
24.00 -2.3451 1.0778
26.00 -2.3236 1.0600
28.00 -2.1784 1.0165
30.00 -2.0214 0.9775
39.00 -2.1109 1.0155
48.00 -2.0362 0.9931
57.00 -2.0709 1.0023
66.00 -2.0588 0.9995
75.00 -2.0616 1.0000
84.00 -2.0615 1.0001
93.00 -2.0611 0.9999
102.00 -2.0614 1.0000
111.00 -2.0613 1.0000
120.00 -2.0613 1.0000
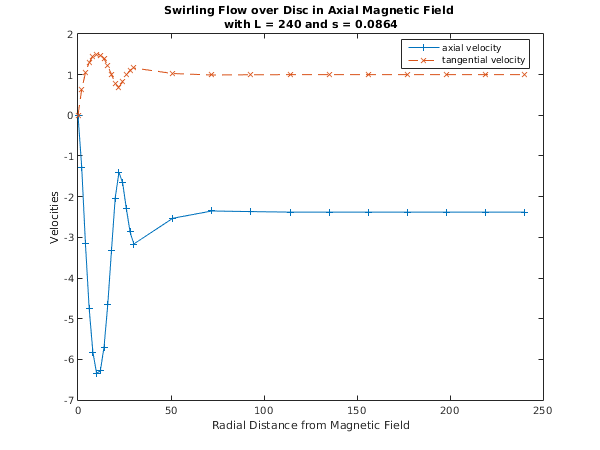
Tolerance = 1.0e-05, L = 240.000, S = 0.0864
Used a mesh of 81 points
Maximum error = 3.30e-07 in interval 19 for component 2
Solution on original interval:
x f g
0.00 0.0000 0.0000
2.00 -1.2756 0.6404
4.00 -3.1604 1.0463
6.00 -4.7459 1.3011
8.00 -5.8265 1.4467
10.00 -6.3412 1.5036
12.00 -6.2862 1.4824
14.00 -5.6976 1.3886
16.00 -4.6568 1.2263
18.00 -3.3226 1.0042
20.00 -2.0328 0.7718
22.00 -1.4035 0.6943
24.00 -1.6603 0.8218
26.00 -2.2975 0.9928
28.00 -2.8661 1.1139
30.00 -3.1641 1.1641
51.00 -2.5307 1.0279
72.00 -2.3520 0.9919
93.00 -2.3674 0.9975
114.00 -2.3799 1.0003
135.00 -2.3800 1.0002
156.00 -2.3792 1.0000
177.00 -2.3791 1.0000
198.00 -2.3792 1.0000
219.00 -2.3792 1.0000
240.00 -2.3792 1.0000