NAG Toolbox: nag_quad_md_adapt_multi (d01ea)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{a}\left(\mathbf{ndim}\right)$ – double array

The lower limits of integration, $a_i$, for $\mathit{i}=1,2,\dots ,n$.

2:     $\mathrm{b}\left(\mathbf{ndim}\right)$ – double array

The upper limits of integration, $b_i$, for $\mathit{i}=1,2,\dots ,n$.

3:     $\mathrm{mincls}$ – int64int32nag_int scalar

Must be set either to the minimum number of funsub calls to be allowed, in which case $\mathbf{mincls}\ge 0$ or to a negative value. In this case, the function continues the calculation started in a previous call with the same integrands and integration limits: no arguments other than mincls, maxcls, absreq, relreq or ifail must be changed between the calls.

4:     $\mathrm{maxcls}$ – int64int32nag_int scalar

The maximum number of funsub calls to be allowed. In the continuation case this is the number of new funsub calls to be allowed.

Constraints:

• $\mathbf{maxcls}\ge \mathbf{mincls}$;
• $\mathbf{maxcls}\ge r$;
• $\text{where }r=2^n+2n^2+2n+1\text{, if }n<11\text{, or }r=1+n\left(4n^2-6n+14\right)/3\text{, if }n\ge 11$.

5:     $\mathrm{nfun}$ – int64int32nag_int scalar

$m$, the number of integrands.

Constraint: $\mathbf{nfun}\ge 1$.

6:     $\mathrm{funsub}$ – function handle or string containing name of m-file

funsub must evaluate the integrands $f_i$ at a given point.

[f] = funsub(ndim, z, nfun)

Input Parameters

1:     $\mathrm{ndim}$ – int64int32nag_int scalar

$n$, the number of dimensions of the integrals.

2:     $\mathrm{z}\left(\mathbf{ndim}\right)$ – double array

The coordinates of the point at which the integrands must be evaluated.

3:     $\mathrm{nfun}$ – int64int32nag_int scalar

$m$, the number of integrands.

Output Parameters

1:     $\mathrm{f}\left(\mathbf{nfun}\right)$ – double array

The value of the $i$th integrand at the given point.

7:     $\mathrm{absreq}$ – double scalar

The absolute accuracy required by you.

Constraint: $\mathbf{absreq}\ge 0.0$.

8:     $\mathrm{relreq}$ – double scalar

The relative accuracy required by you.

Constraint: $\mathbf{relreq}\ge 0.0$.

9:     $\mathrm{wrkstr}\left(\mathbf{lenwrk}\right)$ – double array

If $\mathbf{mincls}<0$, wrkstr must be unchanged from the previous call of nag_quad_md_adapt_multi (d01ea).

Optional Input Parameters

1:     $\mathrm{ndim}$ – int64int32nag_int scalar

Default: the dimension of the arrays a, b. (An error is raised if these dimensions are not equal.)

$n$, the number of dimensions of the integrals.

Constraint: $\mathbf{ndim}\ge 1$.

2:     $\mathrm{lenwrk}$ – int64int32nag_int scalar

Suggested value: $\mathbf{lenwrk}\ge 6n+9m+\left(n+m+2\right)\left(1+p/r\right)$, where $p$ is the value of maxcls and $r$ is defined under maxcls. If lenwrk is significantly smaller than this, the function will not work as efficiently and may even fail.

Default: the dimension of the array wrkstr.

The dimension of the array wrkstr.

Constraint: $\mathbf{lenwrk}\ge 8\times \mathbf{ndim}+11\times \mathbf{nfun}+3$.

Output Parameters

1:     $\mathrm{mincls}$ – int64int32nag_int scalar

Gives the number of funsub calls actually used by nag_quad_md_adapt_multi (d01ea). For the continuation case ($\mathbf{mincls}<0$ on entry) this is the number of new funsub calls on the current call to nag_quad_md_adapt_multi (d01ea).

2:     $\mathrm{wrkstr}\left(\mathbf{lenwrk}\right)$ – double array

Contains information about the current subdivision which could be used in a continuation call.

3:     $\mathrm{finest}\left(\mathbf{nfun}\right)$ – double array

$\mathbf{finest}\left(\mathit{i}\right)$ specifies the best estimate obtained from the $\mathit{i}$th integral, for $\mathit{i}=1,2,\dots ,m$.

4:     $\mathrm{absest}\left(\mathbf{nfun}\right)$ – double array

$\mathbf{absest}\left(\mathit{i}\right)$ specifies the estimated absolute accuracy of $\mathbf{finest}\left(\mathit{i}\right)$, for $\mathit{i}=1,2,\dots ,m$.

5:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.

W  $\mathbf{ifail}=1$

maxcls was too small for nag_quad_md_adapt_multi (d01ea) to obtain the required accuracy. The arrays finest and absest respectively contain current estimates for the integrals and errors.

W  $\mathbf{ifail}=2$

lenwrk is too small for the function to continue. The arrays finest and absest respectively contain current estimates for the integrals and errors.

W  $\mathbf{ifail}=3$

On a continuation call, maxcls was set too small to make any progress. Increase maxcls before calling nag_quad_md_adapt_multi (d01ea) again.

   $\mathbf{ifail}=4$

On entry,	$\mathbf{ndim}<1$,
or	$\mathbf{nfun}<1$,
or	$\mathbf{maxcls}<\mathbf{mincls}$,
or	$\mathbf{maxcls}<r$ (see maxcls),
or	$\mathbf{absreq}<0.0$,
or	$\mathbf{relreq}<0.0$,
or	$\mathbf{lenwrk}<8\times \mathbf{ndim}+11\times \mathbf{nfun}+3$.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Example

Open in the MATLAB editor: d01ea_example

function d01ea_example


fprintf('d01ea example results\n\n');

% Initialize variables and arrays.
nfun = int64(10);
ndim = 4;
absreq = 0;
relreq = 1e-3;
mincls = int64(0);
ircls = 2^ndim+2*ndim*ndim+2*ndim+1;
maxcls = int64(ircls);
lenwrk = 6*ndim+9*nfun+(ndim+nfun+2)*(1+maxcls/ircls);
ncall = 1;
a = zeros(1, ndim);
b = ones(1, ndim);
wrkstr = zeros(lenwrk, 1);
mkeep = zeros(1,1);
fkeep = zeros(1,1);
akeep = zeros(1,1);

% Factor for scaling the maxcls parameter (which controls the maximum
% number of times f is to be called by d01ea).
if (ndim < 10)
    mulfac = 2^ndim;
else
    mulfac = 2*(ndim^3);
end

% Turn off warnings from NAG routines, catching them instead.
wstat = warning();
warning('OFF');
% First call: the initial parameter values are set up to demonstrate the
% continuation facility of the routine; it should exit with ifail = 1
% indicating that maxcls is too small.
% Loop until ifail is not 1 or 3 (i.e. maxcls is big enough).
ifail = int64(1);
while (ifail == 1 || ifail == 3)
    [mincls, wrkstr, finest, absest, ifail] = ...
        d01ea(a, b, mincls, maxcls, nfun, @f, absreq, relreq, wrkstr);

    % Is it big enough yet?  Output appropriate message.
    if ifail ~= 0
        fprintf('maxcls = %7d mincls = %7d  ifail = %d \n\n', maxcls, ...
                mincls, ifail);
    else
        fprintf('Success: %7d user function calls in last call\n\n', mincls);
    end

    % Store results for plotting.
    fkeep(1:nfun,ncall) = finest(1:nfun);
    akeep(1:nfun,ncall) = absest(1:nfun);
    mkeep(ncall,1) = mincls;

    % Prepare for next call of routine.
    mincls = int64(-1);
    maxcls = maxcls * mulfac;
    ncall = ncall + 1;
    if ifail ~= 0
        fprintf('  .. increasing maxcls to %7d\n\n', maxcls);
    end
end
warning(wstat);

% Turn NAG warnings back to origianl setting.
% Plot results.
fig1 = figure;
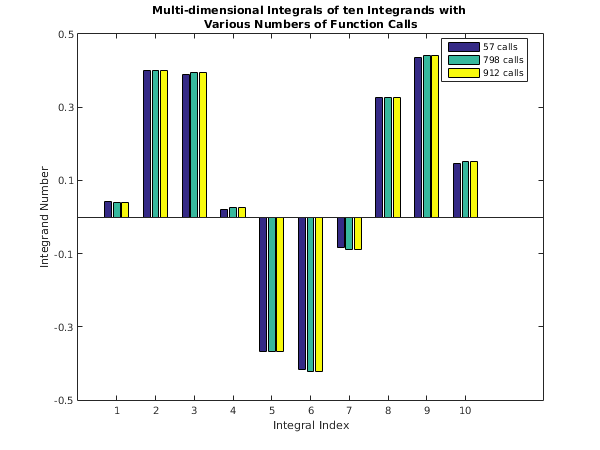
display_plot(fkeep, mkeep, 'Integrand Number');
fig2 = figure;
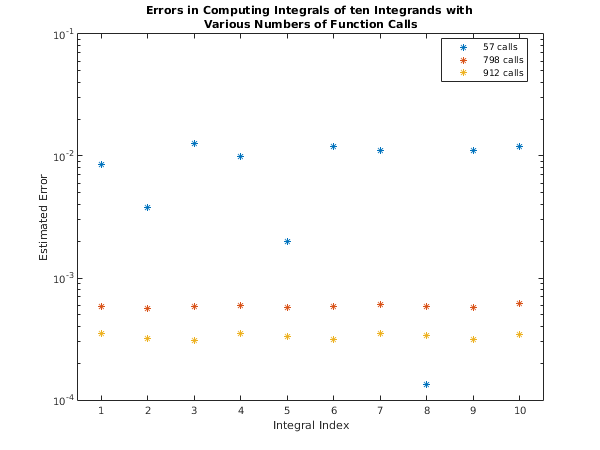
display_plot(akeep, mkeep, 'Estimated Error');


function f = f(ndim, z, nfun)
% Evaluate the integrands.
f = zeros(nfun,1);
sm = 0;
for n=1:ndim
    sm = sm + double(n)*z(n);
end
for k=1:nfun
    f(k) = log(sm)*sin(double(k)+sm);
end

function display_plot(data, labels, ylabelString)
% Formatting for title and axis labels.
% Use bars to plot intregral data and points on logscale for errors.
if strncmp(ylabelString, 'Integrand', 9)
    bar(data,'group');
    title({'Multi-dimensional Integrals of ten Integrands with ', ...
        'Various Numbers of Function Calls'});
    set(gca, 'YTick', [-0.5 -0.3 -0.1 0.1 0.3 0.5]);
else
    plot(data,'*');
    title({'Errors in Computing Integrals of ten Integrands with ', ...
        'Various Numbers of Function Calls'});
    set(gca, 'YScale', 'log');
    set(gca, 'XLim', [0.5 10.5]);
end
xlabel('Integral Index');
ylabel(ylabelString);
% Add a legend.
legend([num2str(labels(1)) ' calls'], ...
    [num2str(labels(2)) ' calls'], ...
    [num2str(labels(3)) ' calls'], 'Location', 'Best')

d01ea example results

maxcls =      57 mincls =      57  ifail = 1 

  .. increasing maxcls to     912

maxcls =     912 mincls =     798  ifail = 1 

  .. increasing maxcls to   14592

Success:     912 user function calls in last call