PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_quad_1d_gauss_wgen (d01bc)
Purpose
nag_quad_1d_gauss_wgen (d01bc) returns the weights (normal or adjusted) and abscissae for a Gaussian integration rule with a specified number of abscissae. Six different types of Gauss rule are allowed.
Syntax
Description
nag_quad_1d_gauss_wgen (d01bc) returns the weights
and abscissae
for use in the summation
which approximates a definite integral (see
Davis and Rabinowitz (1975) or
Stroud and Secrest (1966)). The following types are provided:
| (a) |
Gauss–Legendre
Constraint:
. |
| (b) |
Gauss–Jacobi
normal weights:
adjusted weights:
Constraint:
, , . |
| (c) |
Exponential Gauss
normal weights:
adjusted weights:
Constraint:
, . |
| (d) |
Gauss–Laguerre
normal weights:
adjusted weights:
Constraint:
, . |
| (e) |
Gauss–Hermite
normal weights:
adjusted weights:
Constraint:
, . |
| (f) |
Rational Gauss
normal weights:
adjusted weights:
Constraint:
, , . |
In the above formulae, stands for any polynomial of degree or less in .
The method used to calculate the abscissae involves finding the eigenvalues of the appropriate tridiagonal matrix (see
Golub and Welsch (1969)). The weights are then determined by the formula
where
is the
th orthogonal polynomial with respect to the weight function over the appropriate interval.
The weights and abscissae produced by
nag_quad_1d_gauss_wgen (d01bc) may be passed to
nag_quad_md_gauss (d01fb), which will evaluate the summations in one or more dimensions.
References
Davis P J and Rabinowitz P (1975) Methods of Numerical Integration Academic Press
Golub G H and Welsch J H (1969) Calculation of Gauss quadrature rules Math. Comput. 23 221–230
Stroud A H and Secrest D (1966) Gaussian Quadrature Formulas Prentice–Hall
Parameters
Compulsory Input Parameters
- 1:
– int64int32nag_int scalar
-
Indicates the type of quadrature rule.
- Gauss–Legendre, with normal weights.
- Gauss–Jacobi, with normal weights.
- Gauss–Jacobi, with adjusted weights.
- Exponential Gauss, with normal weights.
- Exponential Gauss, with adjusted weights.
- Gauss–Laguerre, with normal weights.
- Gauss–Laguerre, with adjusted weights.
- Gauss–Hermite, with normal weights.
- Gauss–Hermite, with adjusted weights.
- Rational Gauss, with normal weights.
- Rational Gauss, with adjusted weights.
Constraint:
, , , , , , , , , or .
- 2:
– double scalar
- 3:
– double scalar
- 4:
– double scalar
- 5:
– double scalar
-
The parameters
,
,
and
which occur in the quadrature formulae.
c is not used if
;
d is not used unless
,
,
or
. For some rules
c and
d must not be too large (see
Error Indicators and Warnings).
- 6:
– int64int32nag_int scalar
-
, the number of weights and abscissae to be returned. If
or
and
, an odd value of
n may raise problems (see
).
Constraint:
.
Optional Input Parameters
None.
Output Parameters
- 1:
– double array
-
- 2:
– double array
-
- 3:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
- W
-
The algorithm for computing eigenvalues of a tridiagonal matrix has failed to obtain convergence. If the soft fail option is used, the values of the weights and abscissae on return are indeterminate.
-
-
| On entry, | , |
| or | , |
| or | . |
If the soft fail option is used, weights and abscissae are returned as zero.
-
-
a,
b,
c or
d is not in the allowed range:
- if , ;
- if , or or or ;
- if , or ;
- if , or or ;
- if , or or ;
- if , or or .
Here is the (machine-dependent) largest integer value such that can be computed without overflow.
If the soft fail option is used, weights and abscissae are returned as zero.
- W
-
One or more of the weights are larger than
, the largest floating-point number on this machine.
is given by the function
nag_machine_real_largest (x02al). If the soft fail option is used, the overflowing weights are returned as
. Possible solutions are to use a smaller value of
n; or, if using adjusted weights, to change to normal weights.
- W
-
One or more of the weights are too small to be distinguished from zero on this machine. If the soft fail option is used, the underflowing weights are returned as zero, which may be a usable approximation. Possible solutions are to use a smaller value of
n; or, if using normal weights, to change to adjusted weights.
- W
-
Exponential Gauss or Gauss–Hermite adjusted weights with
n odd and
. Theoretically, in these cases:
- for , the central adjusted weight is infinite, and the exact function is zero at the central abscissa.
- for , the central adjusted weight is zero, and the exact function is infinite at the central abscissa.
In either case, the contribution of the central abscissa to the summation is indeterminate.
In practice, the central weight may not have overflowed or underflowed, if there is sufficient rounding error in the value of the central abscissa.
If the soft fail option is used, the weights and abscissa returned may be usable; you must be particularly careful not to ‘round’ the central abscissa to its true value without simultaneously ‘rounding’ the central weight to zero or as appropriate, or the summation will suffer. It would be preferable to use normal weights, if possible.
Note: remember that, when switching from normal weights to adjusted weights or vice versa, redefinition of is involved.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
The accuracy depends mainly on , with increasing loss of accuracy for larger values of . Typically, one or two decimal digits may be lost from machine accuracy with , and three or four decimal digits may be lost for .
Further Comments
The major portion of the time is taken up during the calculation of the eigenvalues of the appropriate tridiagonal matrix, where the time is roughly proportional to .
Example
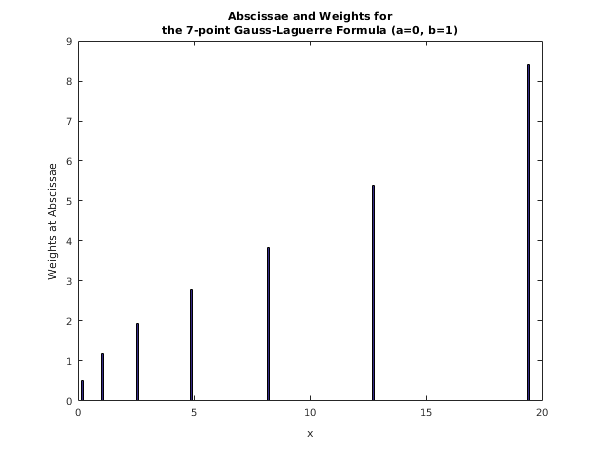
This example returns the abscissae and (adjusted) weights for the seven-point Gauss–Laguerre formula.
Open in the MATLAB editor:
d01bc_example
function d01bc_example
fprintf('d01bc example results\n\n');
itype = -3;
a =0;
b = 1;
c = 0;
d = 0;
n = 7;
[weight, abscis, ifail] = d01bc(int64(itype), a, b, c, d, int64(n));
if ifail ~= 0
error('Warning: d01bc returned with ifail = %1d ',ifail);
end
fprintf(' Laguerre formula, %d points \n', n);
fprintf(' Abscissae Weights \n')
for i = 1:n
fprintf(' %10.5e %10.5e \n',abscis(i),weight(i))
end
fig1 = figure;
display_plot(abscis, weight);
function plot(abscis, weight)
bar1 = bar(abscis, weight);
set(bar1, 'BarWidth', 0.1);
xlabel('x');
ylabel('Weights at Abscissae');
function display_plot(abscis, weight)
bar1 = bar(abscis, weight);
set(bar1, 'BarWidth', 0.1);
title({'Abscissae and Weights for',...
'the 7-point Gauss-Laguerre Formula (a=0, b=1)'});
xlabel('x');
ylabel('Weights at Abscissae');
d01bc example results
Laguerre formula, 7 points
Abscissae Weights
1.93044e-01 4.96478e-01
1.02666e+00 1.17764e+00
2.56788e+00 1.91825e+00
4.90035e+00 2.77185e+00
8.18215e+00 3.84125e+00
1.27342e+01 5.38068e+00
1.93957e+01 8.40543e+00
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015