The E02 Chapter - Fitting a set of points with a cubic spline

A common task in many areas of science is to find a function which approximates a set of data points. The data may contain random perturbations - such as measurement errors - which it is desirable to smooth out. Here, we investigate the one-dimensional case, where we seek to find a cubic spline curve f(x) which approximates a set of data values given on the x-axis. The NAG routine which does this is e02be, while the supplementary routine e02bb can be used to evaluate the spline at any point, given the results from e02be.

Cubic splines are knitted together at points on the x axis called knots. The art of choosing the best places for the knots can be a difficult one to master - choosing the knots in the wrong place may lead to a fitted curve with wild oscillations. The NAG routine e02be removes the need to choose these knots from the user. Instead, a single parameter is specified to control the trade-off between closeness and smoothness of fit. A small value for this smoothing parameter, named s in e02be, will give a closer fit to the data, but the exact meaning of "small" in this context will vary according to the particular data set. In the extremes, a value of s = 0 will produce an interpolating spline, while a very large value will produce the weighted least-squares cubic polynomial approximation to the points.

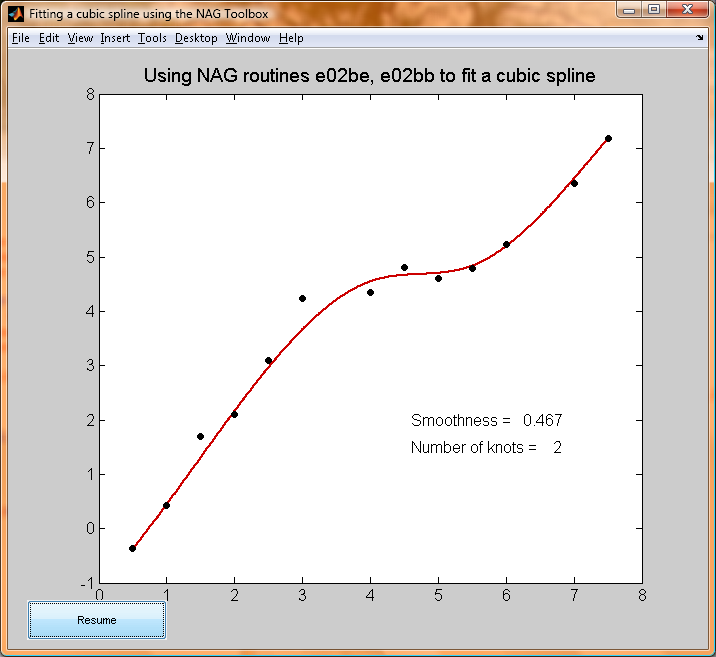
Fitting a cubic spline through a set of data points.