NAG Library Routine Document

Integer, Intent (In)	::	n, ns, ne, nnz, icol(nnz)
Integer, Intent (Inout)	::	irow(nnz), ifail
Integer, Intent (Out)	::	path(n), iwork(3*n+1)
Real (Kind=nag_wp), Intent (In)	::	d(nnz)
Real (Kind=nag_wp), Intent (Out)	::	splen, work(2*n)
Logical, Intent (In)	::	direct

C Header Interface

#include <nagmk26.h>

void	h03adf_ (const Integer n, const Integer ns, const Integer ne, const logical direct, const Integer nnz, const double d[], Integer irow[], const Integer icol[], double splen, Integer path[], Integer iwork[], double work[], Integer *ifail)

3

Description

h03adf attempts to find the shortest path through a directed or undirected acyclic network, which consists of a set of points called vertices and a set of curves called arcs that connect certain pairs of distinct vertices. An acyclic network is one in which there are no paths connecting a vertex to itself. An arc whose origin vertex is

i

and whose destination vertex is

j

can be written as

i \to j

. In an undirected network the arcs

i \to j

and

j \to i

are equivalent (i.e.,

i \leftrightarrow j

), whereas in a directed network they are different. Note that the shortest path may not be unique and in some cases may not even exist (e.g., if the network is disconnected).

The network is assumed to consist of

n

vertices which are labelled by the integers

1, 2, \dots, n

. The lengths of the arcs between the vertices are defined by the

n

n

distance matrix

d

, in which the element

d_{i j}

gives the length of the arc

i \to j

;

d_{i j} = 0

if there is no arc connecting vertices

i

and

j

(as is the case for an acyclic network when

i = j

). Thus the matrix

D

is usually sparse. For example, if

n = 4

and the network is directed, then

d = (\begin{matrix} 0 & d_{12} & d_{13} & d_{14} \\ d_{21} & 0 & d_{23} & d_{24} \\ d_{31} & d_{32} & 0 & d_{34} \\ d_{41} & d_{42} & d_{43} & 0 \end{matrix}) .

If the network is undirected,

d

is symmetric since

d_{i j} = d_{j i}

(i.e., the length of the arc

i \to j \equiv

the length of the arc

j \to i

The method used by h03adf is described in detail in Section 9.

4

References

Dijkstra E W (1959) A note on two problems in connection with graphs Numer. Math. 1 269–271

5

Arguments

1: $n$ – IntegerInput

On entry:

n

, the number of vertices.

Constraint:

n \geq 2

2: $ns$ – IntegerInput

3: $ne$ – IntegerInput

On entry:

n_{s}

and

n_{e}

, the labels of the first and last vertices, respectively, between which the shortest path is sought.

Constraints:

$1 \leq ns \leq n$ ;
$1 \leq ne \leq n$ ;
$ns \neq ne$ .

4: $direct$ – LogicalInput

On entry: indicates whether the network is directed or undirected.

$direct = .TRUE.$: The network is directed.
$direct = .FALSE.$: The network is undirected.

5: $nnz$ – IntegerInput

On entry: the number of nonzero elements in the distance matrix

D

Constraints:

if $direct = .TRUE.$ , $1 \leq nnz \leq n \times (n - 1)$ ;
if $direct = .FALSE.$ , $1 \leq nnz \leq n \times (n - 1) / 2$ .

6: $d (nnz)$ – Real (Kind=nag_wp) arrayInput

On entry: the nonzero elements of the distance matrix

D

, ordered by increasing row index and increasing column index within each row. More precisely,

d (k)

must contain the value of the nonzero element with indices (

irow (k), icol (k)

); this is the length of the arc from the vertex with label

irow (k)

to the vertex with label

icol (k)

. Elements with the same row and column indices are not allowed. If

direct = .FALSE.

, then only those nonzero elements in the strict upper triangle of

d

need be supplied since

d_{i j} = d_{j i}

. (f11zaf may be used to sort the elements of an arbitrarily ordered matrix into the required form. This is illustrated in Section 10.)

Constraint:

d (k) > 0.0

, for

k = 1, 2, \dots, nnz

7: $irow (nnz)$ – Integer arrayInput

8: $icol (nnz)$ – Integer arrayInput

On entry:

irow (k)

and

icol (k)

must contain the row and column indices, respectively, for the nonzero element stored in

d (k)

Constraints:

irow and icol must satisfy the following constraints (which may be imposed by a call to f11zaf):

$irow (k - 1) < irow (k)$ ;
$irow (k - 1) = irow (k)$ and $icol (k - 1) < icol (k)$ , for $k = 2, 3, \dots, nnz$ .

In addition, if

direct = .TRUE.

1 \leq irow (k) \leq n

1 \leq icol (k) \leq n

and

irow (k) \neq icol (k)

;

if $direct = .FALSE.$ , $1 \leq irow (k) < icol (k) \leq n$ .

9: $splen$ – Real (Kind=nag_wp)Output

On exit: the length of the shortest path between the specified vertices

n_{s}

and

n_{e}

10: $path (n)$ – Integer arrayOutput

On exit: contains details of the shortest path between the specified vertices

n_{s}

and

n_{e}

. More precisely,

ns = path (1) \to path (2) \to \dots \to path (p) = ne

for some

p \leq n

. The remaining

(n - p)

elements are set to zero.

11: $iwork (3 \times n + 1)$ – Integer arrayWorkspace

12: $work (2 \times n)$ – Real (Kind=nag_wp) arrayWorkspace

13: $ifail$ – IntegerInput/Output

On entry: ifail must be set to

0

- 1 or 1

. If you are unfamiliar with this argument you should refer to Section 3.4 in How to Use the NAG Library and its Documentation for details.

For environments where it might be inappropriate to halt program execution when an error is detected, the value

- 1 or 1

is recommended. If the output of error messages is undesirable, then the value

1

is recommended. Otherwise, if you are not familiar with this argument, the recommended value is

0

. When the value $- 1 or 1$ is used it is essential to test the value of ifail on exit.

On exit:

ifail = 0

unless the routine detects an error or a warning has been flagged (see Section 6).

6

Error Indicators and Warnings

If on entry

ifail = 0

- 1

, explanatory error messages are output on the current error message unit (as defined by x04aaf).

Errors or warnings detected by the routine:

$ifail = 1$

On entry,	$n < 2$ ,
or	$ns < 1$ ,
or	$ns > n$ ,
or	$ne < 1$ ,
or	$ne > n$ ,
or	$ns = ne$ .

$ifail = 2$

On entry,	$nnz > n \times (n - 1)$ when $direct = .TRUE.$ ,
or	$nnz > n \times (n - 1) / 2$ when $direct = .FALSE.$ ,
or	$nnz < 1$ .

$ifail = 3$: On entry, $irow (k) < 1$ or $irow (k) > n$ or $icol (k) < 1$ or $icol (k) > n$ or $irow (k) = icol (k)$ for some $k$ when $direct = .TRUE.$ .

$ifail = 4$: On entry, $irow (k) < 1$ or $irow (k) \geq icol (k)$ or $icol (k) > n$ for some $k$ when $direct = .FALSE.$ .

$ifail = 5$: $d (k) \leq 0.0$ for some $k$ .

$ifail = 6$: On entry, $irow (k - 1) > irow (k)$ or $irow (k - 1) = irow (k)$ and $icol (k - 1) > icol (k)$ for some $k$ .

$ifail = 7$: On entry, $irow (k - 1) = irow (k)$ and $icol (k - 1) = icol (k)$ for some $k$ .

$ifail = 8$: No connected network exists between vertices ns and ne.

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.
See Section 3.9 in How to Use the NAG Library and its Documentation for further information.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.
See Section 3.8 in How to Use the NAG Library and its Documentation for further information.

$ifail = - 999$: Dynamic memory allocation failed.
See Section 3.7 in How to Use the NAG Library and its Documentation for further information.

7

Accuracy

The results are exact, except for the obvious rounding errors in summing the distances in the length of the shortest path.

8

Parallelism and Performance

h03adf is not threaded in any implementation.

9

Further Comments

h03adf is based upon Dijkstra's algorithm (see Dijkstra (1959)), which attempts to find a path

n_{s} \to n_{e}

between two specified vertices

n_{s}

and

n_{e}

of shortest length

d (n_{s}, n_{e})

The algorithm proceeds by assigning labels to each vertex, which may be temporary or permanent. A temporary label can be changed, whereas a permanent one cannot. For example, if vertex

p

has a permanent label

(q, r)

, then

r

is the distance

d (n_{s}, r)

and

q

is the previous vertex on a shortest length

n_{s} \to p

path. If the label is temporary, then it has the same meaning but it refers only to the shortest

n_{s} \to p

path found so far. A shorter one may be found later, in which case the label may become permanent.

The algorithm consists of the following steps.

Assign the permanent label

(-, 0)

to vertex

n_{s}

and temporary labels

(-, \infty)

to every other vertex. Set

k = n_{s}

and go to 2.

Consider each vertex

y

adjacent to vertex

k

with a temporary label in turn. Let the label at

k

(p, q)

and at

y (r, s)

. If

q + d_{k y} < s

, then a new temporary label

(k, q + d_{k y})

is assigned to vertex

y

; otherwise no change is made in the label of

y

. When all vertices

y

with temporary labels adjacent to

k

have been considered, go to 3.

From the set of temporary labels, select the one with the smallest second component and declare that label to be permanent. The vertex it is attached to becomes the new vertex

k

. If

k = n_{e}

go to 4. Otherwise go to 2 unless no new vertex can be found (e.g., when the set of temporary labels is ‘empty’ but

k \neq n_{e}

, in which case no connected network exists between vertices

n_{s}

and

n_{e}

To find the shortest path, let

(y, z)

denote the label of vertex

n_{e}

. The column label (

z

) gives

d (n_{s}, n_{e})

while the row label (

y

) then links back to the previous vertex on a shortest length

n_{s} \to n_{e}

path. Go to vertex

y

. Suppose that the (permanent) label of vertex

y

(w, x)

, then the next previous vertex is

w

on a shortest length

n_{s} \to y

path. This process continues until vertex

n_{s}

is reached. Hence the shortest path is

n_{s} \to \dots \to w \to y \to n_{e},

which has length

d (n_{s}, n_{e})

10

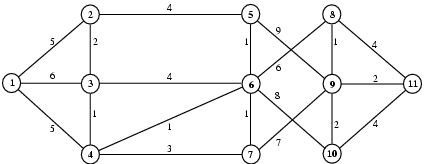
Example

This example finds the shortest path between vertices

1

and

11

for the undirected network

Figure 1

NAG Library Routine Document

h03adf (shortestpath)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1

Purpose

2

Specification

3

Description

4

References

5

Arguments

6

Error Indicators and Warnings

7

Accuracy

8

Parallelism and Performance

9

Further Comments

10

Example

10.1

Program Text

10.2

Program Data

10.3

Program Results