NAG Library ManualKeyword Search:

NAG Library Routine Document

s15adf (erfc_real)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

▸▿ 10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1

Purpose

s15adf returns the value of the complementary error function,

erfc (x)

, via the function name.

2

Specification

Fortran Interface

Function s15adf (

x, ifail)

Real (Kind=nag_wp)	::	s15adf
Integer, Intent (Inout)	::	ifail
Real (Kind=nag_wp), Intent (In)	::	x

C Header Interface

#include nagmk26.h

double

s15adf_ ( const double *x, Integer *ifail)

3

Description

s15adf calculates an approximate value for the complement of the error function

erfc (x) = \frac{2}{\sqrt{π}} \int_{x}^{\infty} e^{- t^{2}} d t = 1 - \erf (x) .

Let

\hat{x}

be the root of the equation

erfc (x) - \erf (x) = 0

(then

\hat{x} \approx 0.46875

). For

|x| \leq \hat{x}

the value of

erfc (x)

is based on the following rational Chebyshev expansion for

\erf (x)

\erf (x) \approx x R_{ℓ, m} (x^{2}),

where

R_{ℓ, m}

denotes a rational function of degree

ℓ

in the numerator and

m

in the denominator.

For

|x| > \hat{x}

the value of

erfc (x)

is based on a rational Chebyshev expansion for

erfc (x)

: for

\hat{x} < |x| \leq 4

the value is based on the expansion

erfc (x) \approx e^{x^{2}} R_{ℓ, m} (x);

and for

|x| > 4

it is based on the expansion

erfc (x) \approx \frac{e^{x^{2}}}{x} (\frac{1}{\sqrt{π}} + \frac{1}{x^{2}} R_{ℓ, m} (1 / x^{2})) .

For each expansion, the specific values of

ℓ

and

m

are selected to be minimal such that the maximum relative error in the expansion is of the order

10^{- d}

, where

d

is the maximum number of decimal digits that can be accurately represented for the particular implementation (see x02bef).

For

|x| \geq x_{hi}

there is a danger of setting underflow in

erfc (x)

(the value of

x_{hi}

is given in the Users' Note for your implementation). For

x \geq x_{hi}

, s15adf returns

erfc (x) = 0

; for

x \leq - x_{hi}

it returns

erfc (x) = 2

4

References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

Cody W J (1969) Rational Chebyshev approximations for the error function Math.Comp. 23 631–637

5

Arguments

1: $x$ – Real (Kind=nag_wp)Input: On entry: the argument $x$ of the function.
2: $ifail$ – IntegerInput/Output: On entry: ifail must be set to $0$ , $- 1 or 1$ . If you are unfamiliar with this argument you should refer to Section 3.4 in How to Use the NAG Library and its Documentation for details.
For environments where it might be inappropriate to halt program execution when an error is detected, the value $- 1 or 1$ is recommended. If the output of error messages is undesirable, then the value $1$ is recommended. Otherwise, if you are not familiar with this argument, the recommended value is $0$ . When the value $- 1 or 1$ is used it is essential to test the value of ifail on exit.

On exit: $ifail = 0$ unless the routine detects an error or a warning has been flagged (see Section 6).

6

Error Indicators and Warnings

There are no failure exits from s15adf. The argument ifail has been included for consistency with other routines in this chapter.

7

Accuracy

δ

and

ε

are relative errors in the argument and result, respectively, then in principle

|ε| ≃ |\frac{2 x e^{- x^{2}}}{\sqrt{π} erfc (x)} δ| .

That is, the relative error in the argument,

x

, is amplified by a factor

\frac{2 x e^{- x^{2}}}{\sqrt{π} erfc (x)}

in the result.

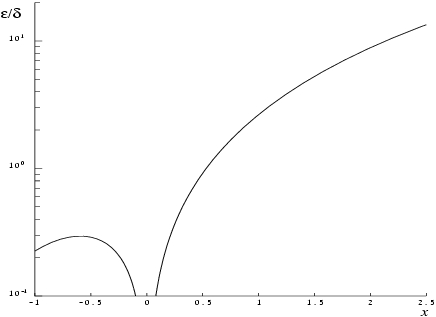
The behaviour of this factor is shown in Figure 1.

Figure 1

It should be noted that near

x = 0

this factor behaves as

\frac{2 x}{\sqrt{π}}

and hence the accuracy is largely determined by the machine precision. Also for large negative

x

, where the factor is

\sim \frac{x e^{- x^{2}}}{\sqrt{π}}

, accuracy is mainly limited by machine precision. However, for large positive

x

, the factor becomes

\sim 2 x^{2}

and to an extent relative accuracy is necessarily lost. The absolute accuracy

E

is given by

E ≃ \frac{2 x e^{- x^{2}}}{\sqrt{π}} δ

so absolute accuracy is guaranteed for all

x

8

Parallelism and Performance

s15adf is not threaded in any implementation.

9

Further Comments

None.

10

Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

NAG Library Routine Document

s15adf (erfc_real)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results