| SUBROUTINE D06AAF ( |
NVB, NVMAX, NEDGE, EDGE, NV, NELT, COOR, CONN, BSPACE, SMOOTH, COEF, POWER, ITRACE, RWORK, LRWORK, IWORK, LIWORK, IFAIL) |
| INTEGER |
NVB, NVMAX, NEDGE, EDGE(3,NEDGE), NV, NELT, CONN(3,2*(NVMAX-1)), ITRACE, LRWORK, IWORK(LIWORK), LIWORK, IFAIL |
| REAL (KIND=nag_wp) |
COOR(2,NVMAX), BSPACE(NVB), COEF, POWER, RWORK(LRWORK) |
| LOGICAL |
SMOOTH |
|
D06AAF generates the set of interior vertices using a process based on a simple incremental method. A smoothing of the mesh is optionally available. For more details about the triangulation method, consult the
D06 Chapter Introduction as well as
George and Borouchaki (1998).
This routine is derived from material in the MODULEF package from INRIA (Institut National de Recherche en Informatique et Automatique).
- 1: NVB – INTEGERInput
On entry: the number of vertices in the input boundary mesh.
Constraint:
.
- 2: NVMAX – INTEGERInput
On entry: the maximum number of vertices in the mesh to be generated.
- 3: NEDGE – INTEGERInput
On entry: the number of boundary edges in the input mesh.
Constraint:
.
- 4: EDGE(,NEDGE) – INTEGER arrayInput
On entry: the specification of the boundary edges. and contain the vertex numbers of the two end points of the th boundary edge. is a user-supplied tag for the th boundary edge and is not used by D06AAF.
Constraint:
and , for and .
- 5: NV – INTEGEROutput
On exit: the total number of vertices in the output mesh (including both boundary and interior vertices). If , no interior vertices will be generated and .
- 6: NELT – INTEGEROutput
On exit: the number of triangular elements in the mesh.
- 7: COOR(,NVMAX) – REAL (KIND=nag_wp) arrayInput/Output
On entry: contains the coordinate of the th input boundary mesh vertex; while contains the corresponding coordinate, for .
On exit: will contain the coordinate of the th generated interior mesh vertex; while will contain the corresponding coordinate, for . The remaining elements are unchanged.
- 8: CONN(,) – INTEGER arrayOutput
On exit: the connectivity of the mesh between triangles and vertices. For each triangle
, gives the indices of its three vertices (in anticlockwise order), for and .
- 9: BSPACE(NVB) – REAL (KIND=nag_wp) arrayInput
On entry: the desired mesh spacing (triangle diameter, which is the length of the longer edge of the triangle) near the boundary vertices.
Constraint:
, for .
- 10: SMOOTH – LOGICALInput
On entry: indicates whether or not mesh smoothing should be performed.
If , the smoothing is performed; otherwise no smoothing is performed.
- 11: COEF – REAL (KIND=nag_wp)Input
On entry: the coefficient in the stopping criteria for the generation of interior vertices. This parameter controls the triangle density and the number of triangles generated is in
. The mesh will be finer if
COEF is greater than
and
is a good value.
Suggested value:
.
- 12: POWER – REAL (KIND=nag_wp)Input
On entry: controls the rate of change of the mesh size during the generation of interior vertices. The smaller the value of
POWER, the faster the decrease in element size away from the boundary.
Suggested value:
.
Constraint:
.
- 13: ITRACE – INTEGERInput
On entry: the level of trace information required from D06AAF.
- No output is generated.
- Output from the meshing solver is printed on the current advisory message unit (see X04ABF). This output contains details of the vertices and triangles generated by the process.
You are advised to set , unless you are experienced with finite element mesh generation.
- 14: RWORK(LRWORK) – REAL (KIND=nag_wp) arrayWorkspace
- 15: LRWORK – INTEGERInput
On entry: the dimension of the array
RWORK as declared in the (sub)program from which D06AAF is called.
Constraint:
.
- 16: IWORK(LIWORK) – INTEGER arrayWorkspace
- 17: LIWORK – INTEGERInput
On entry: the dimension of the array
IWORK as declared in the (sub)program from which D06AAF is called.
Constraint:
.
- 18: IFAIL – INTEGERInput/Output
-
On entry:
IFAIL must be set to
,
. If you are unfamiliar with this parameter you should refer to
Section 3.3 in the Essential Introduction for details.
For environments where it might be inappropriate to halt program execution when an error is detected, the value
is recommended. If the output of error messages is undesirable, then the value
is recommended. Otherwise, if you are not familiar with this parameter, the recommended value is
.
When the value is used it is essential to test the value of IFAIL on exit.
On exit:
unless the routine detects an error or a warning has been flagged (see
Section 6).
If on entry
or
, explanatory error messages are output on the current error message unit (as defined by
X04AAF).
Not applicable.
The position of the internal vertices is a function of the positions of the vertices on the given boundary. A fine mesh on the boundary results in a fine mesh in the interior. The algorithm allows you to obtain a denser interior mesh by varying
NVMAX,
BSPACE,
COEF and
POWER. But you are advised to manipulate the last two parameters with care.
You are advised to take care to set the boundary inputs properly, especially for a boundary with multiply connected components. The orientation of the interior boundaries should be in clockwise order and opposite to that of the exterior boundary. If the boundary has only one connected component, its orientation should be anticlockwise.
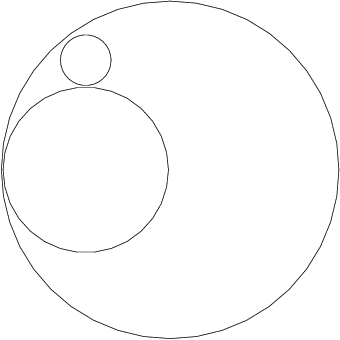
In this example, a geometry with two holes (two interior circles inside an exterior one) is meshed using the simple incremental method (see the
D06 Chapter Introduction). The exterior circle is centred at the origin with a radius
, the first interior circle is centred at the point
with a radius
, and the second one is centred at the point
with a radius
. Note that the points
and
) are points of ‘near tangency’ between the exterior circle and the first and second circles.
The boundary mesh has
vertices and
edges (see
Figure 1). Note that the particular mesh generated could be sensitive to the
machine precision and therefore may differ from one implementation to another.
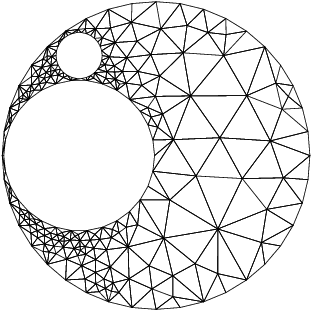
Figure 2 contains the output mesh.
Figure 1: The boundary mesh of the geometry with two holes
Figure 2: Interior mesh of the geometry with two holes