NAG Library Routine Document
S09ABF
1 Purpose
S09ABF returns the value of the inverse circular cosine, , via the function name; the result is in the principal range .
2 Specification
| REAL (KIND=nag_wp) S09ABF |
| INTEGER |
IFAIL |
| REAL (KIND=nag_wp) |
X |
|
3 Description
S09ABF calculates an approximate value for the inverse circular cosine,
. It is based on the Chebyshev expansion
where
.
For .
For .
For .
For is undefined and the routine fails.
4 References
Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications
5 Parameters
- 1: X – REAL (KIND=nag_wp)Input
On entry: the argument of the function.
Constraint:
.
- 2: IFAIL – INTEGERInput/Output
-
On entry:
IFAIL must be set to
,
. If you are unfamiliar with this parameter you should refer to
Section 3.3 in the Essential Introduction for details.
For environments where it might be inappropriate to halt program execution when an error is detected, the value
is recommended. If the output of error messages is undesirable, then the value
is recommended. Otherwise, if you are not familiar with this parameter, the recommended value is
.
When the value is used it is essential to test the value of IFAIL on exit.
On exit:
unless the routine detects an error or a warning has been flagged (see
Section 6).
6 Error Indicators and Warnings
If on entry
or
, explanatory error messages are output on the current error message unit (as defined by
X04AAF).
Errors or warnings detected by the routine:
S09ABF has been called with , for which arccos is undefined. A zero result is returned.
7 Accuracy
If
and
are the relative errors in the argument and the result, respectively, then in principle
The equality should hold if
is greater than the
machine precision (
is due to data errors etc.), but if
is due simply to round-off in the machine it is possible that rounding etc. in internal calculations may lose one extra figure.
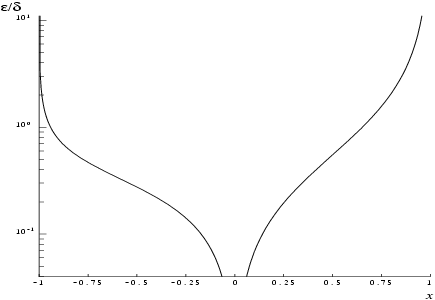
The behaviour of the amplification factor is shown in the graph below.
In the region of this factor tends to zero and the accuracy will be limited by the machine precision. For close to one, , the above analysis is not applicable owing to the fact that both the argument and the result are bounded , .
In the region of we have , that is the result will have approximately half as many correct significant figures as the argument.
In the region , we have that the absolute error in the result, , is given by , that is the result will have approximately half as many decimal places correct as there are correct figures in the argument.
None.
9 Example
This example reads values of the argument from a file, evaluates the function at each value of and prints the results.
9.1 Program Text
Program Text (s09abfe.f90)
9.2 Program Data
Program Data (s09abfe.d)
9.3 Program Results
Program Results (s09abfe.r)