NAG Library Routine Document

S18AEF

+− Contents

1 Purpose

2 Specification

3 Description

4 References

5 Parameters

6 Error Indicators and Warnings

7 Accuracy

8 Further Comments

+− 9 Example

9.1 Program Text

9.2 Program Data

9.3 Program Results

1 Purpose

S18AEF returns the value of the modified Bessel function

I_{0} (x)

, via the function name.

2 Specification

FUNCTION S18AEF (

X, IFAIL)

REAL (KIND=nag_wp) S18AEF

INTEGER	IFAIL
REAL (KIND=nag_wp)	X

3 Description

S18AEF evaluates an approximation to the modified Bessel function of the first kind

I_{0} (x)

Note:

I_{0} (- x) = I_{0} (x)

, so the approximation need only consider

x \geq 0

The routine is based on three Chebyshev expansions:

For

0 < x \leq 4

I_{0} (x) = e^{x} \underset{r = 0}{\sum^{'}} a_{r} T_{r} (t),   where ​ t = 2 (\frac{x}{4}) - 1 .

For

4 < x \leq 12

I_{0} (x) = e^{x} \underset{r = 0}{\sum^{'}} b_{r} T_{r} (t),   where ​ t = \frac{x - 8}{4} .

For

x > 12

I_{0} (x) = \frac{e^{x}}{\sqrt{x}} \underset{r = 0}{\sum^{'}} c_{r} T_{r} (t),   where ​ t = 2 (\frac{12}{x}) - 1 .

For small

x

I_{0} (x) ≃ 1

. This approximation is used when

x

is sufficiently small for the result to be correct to machine precision.

For large

x

, the routine must fail because of the danger of overflow in calculating

e^{x}

4 References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

5 Parameters

1: X – REAL (KIND=nag_wp)Input: On entry: the argument $x$ of the function.
2: IFAIL – INTEGERInput/Output: On entry: IFAIL must be set to $0$ , $- 1 or 1$ . If you are unfamiliar with this parameter you should refer to Section 3.3 in the Essential Introduction for details.
For environments where it might be inappropriate to halt program execution when an error is detected, the value $- 1 or 1$ is recommended. If the output of error messages is undesirable, then the value $1$ is recommended. Otherwise, if you are not familiar with this parameter, the recommended value is $0$ . When the value $- 1 or 1$ is used it is essential to test the value of IFAIL on exit.

On exit: $IFAIL = 0$ unless the routine detects an error or a warning has been flagged (see Section 6).

6 Error Indicators and Warnings

If on entry

IFAIL = 0

- 1

, explanatory error messages are output on the current error message unit (as defined by X04AAF).

Errors or warnings detected by the routine:

$IFAIL = 1$: $|X|$ is too large. On soft failure the routine returns the approximate value of $I_{0} (x)$ at the nearest valid argument. (see the Users' Note for your implementation for details)

7 Accuracy

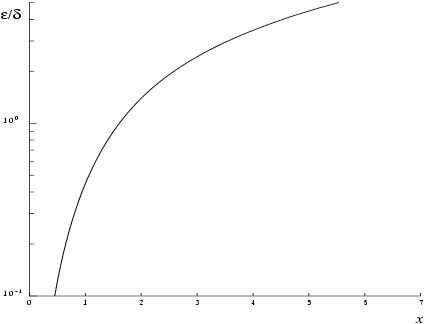
Let

δ

and

ε

be the relative errors in the argument and result respectively.

δ

is somewhat larger than the machine precision (i.e., if

δ

is due to data errors etc.), then

ε

and

δ

are approximately related by:

ε ≃ |\frac{x I_{1} (x)}{I_{0} (x)}| δ .

Figure 1 shows the behaviour of the error amplification factor

|\frac{x I_{1} (x)}{I_{0} (x)}| .

Figure 1

However if

δ

is of the same order as machine precision, then rounding errors could make

ε

slightly larger than the above relation predicts.

For small

x

the amplification factor is approximately

\frac{x^{2}}{2}

, which implies strong attenuation of the error, but in general

ε

can never be less than the machine precision.

For large

x

ε ≃ x δ

and we have strong amplification of errors. However the routine must fail for quite moderate values of

x

, because

I_{0} (x)

would overflow; hence in practice the loss of accuracy for large

x

is not excessive. Note that for large

x

the errors will be dominated by those of the standard function exp.

8 Further Comments

None.

9 Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

NAG Library Routine DocumentS18AEF