For
it uses the Chebyshev expansion
where
.
where
is a machine-dependent constant, details of which are given in the
Users' Note for your implementation.
If on entry
or
, explanatory error messages are output on the current error message unit (as defined by
X04AAF).
If
and
are the relative errors in the argument and result, respectively, then in principle
That is the relative error in the argument,
, is amplified by a factor, approximately
. The equality should hold if
is greater than the
machine precision (
is a result of data errors etc.) but, if
is simply a result of round-off in the machine representation of
, then it is possible that an extra figure may be lost in internal calculation round-off.
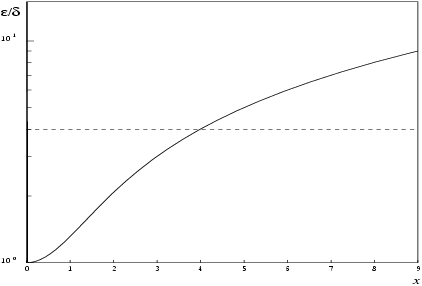
The behaviour of the error amplification factor can be seen in the following graph:
Figure 1
It should be noted that for
where
is the absolute error in the argument.
None.