NAG Library Routine Document

F01LHF

1  Purpose

2  Specification

3  Description

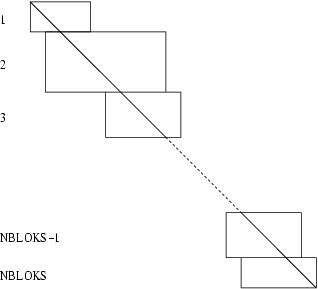
F01LHF factorizes a real almost block diagonal matrix, $A$, by row elimination with alternate row and column pivoting such that no ‘fill-in’ is produced. The code, which is derived from ARCECO described in Diaz et al. (1983), uses Level 1 and Level 2 BLAS. No three successive diagonal blocks may have columns in common and therefore the almost block diagonal matrix must have the form shown in the following diagram:

Figure 1

4  References

5  Parameters

1:     N – INTEGERInput

On entry: $n$, the order of the matrix $A$.

Constraint: $\mathbf{N}>0$.

2:     NBLOKS – INTEGERInput

On entry: $n$, the total number of blocks of the matrix $A$.

Constraint: $0<\mathbf{NBLOKS}\le \mathbf{N}$.

3:     BLKSTR($3$,NBLOKS) – INTEGER arrayInput

On entry: information which describes the block structure of $A$ as follows:

• $\mathbf{BLKSTR}\left(1,k\right)$ must contain the number of rows in the $k$th block, $k=1,2,\dots ,\mathbf{NBLOKS}$;
• $\mathbf{BLKSTR}\left(2,k\right)$ must contain the number of columns in the $k$th block, $k=1,2,\dots ,\mathbf{NBLOKS}$;
• $\mathbf{BLKSTR}\left(3,k\right)$ must contain the number of columns of overlap between the $k$th and $\left(k+1\right)$th blocks, $k=1,2,\dots ,\mathbf{NBLOKS}-1$. $\mathbf{BLKSTR}\left(3,\mathbf{NBLOKS}\right)$ need not be set.

The following conditions delimit the structure of $A$:

• $\mathbf{BLKSTR}\left(1,k\right),\mathbf{BLKSTR}\left(2,k\right)>0\text{, \hspace{1em}}k=1,2,\dots ,\mathbf{NBLOKS}$,
• $\mathbf{BLKSTR}\left(3,k\right)\ge 0\text{, \hspace{1em}}k=1,2,\dots ,\mathbf{NBLOKS}-1$,

(there must be at least one column and one row in each block and a non-negative number of columns of overlap);

• $\mathbf{BLKSTR}\left(3,k-1\right)+\mathbf{BLKSTR}\left(3,k\right)\le \mathbf{BLKSTR}\left(2,k\right)\text{, \hspace{1em}}k=2,3,\dots ,\mathbf{NBLOKS}-1$,

(the total number of columns in overlaps in each block must not exceed the number of columns in that block);

• $\mathbf{BLKSTR}\left(2,1\right)\ge \mathbf{BLKSTR}\left(1,1\right)$,
• $\mathbf{BLKSTR}\left(2,1\right)+{\displaystyle \sum _{k=2}^j}\left[\mathbf{BLKSTR}\left(2,k\right)-\mathbf{BLKSTR}\left(3,k-1\right)\right]\ge {\displaystyle \sum _{k=1}^j}\mathbf{BLKSTR}\left(1,k\right)$, $j=2,3,\dots ,\mathbf{NBLOKS}-1$,
• ${\displaystyle \sum _{k=1}^j}\left[\mathbf{BLKSTR}\left(2,k\right)-\mathbf{BLKSTR}\left(3,k\right)\right]\le {\displaystyle \sum _{k=1}^j}\mathbf{BLKSTR}\left(1,k\right)\text{, \hspace{1em}}j=1,2,\dots ,\mathbf{NBLOKS}-1$,

(the index of the first column of the overlap between the $j$th and $\left(j+1\right)$th blocks must be $\le$ the index of the last row of the $j$th block, and the index of the last column of overlap must be $\ge$ the index of the last row of the $j$th block);

• ${\displaystyle \sum _{k=1}^{\mathbf{NBLOKS}}}\mathbf{BLKSTR}\left(1,k\right)=n$,
• $\mathbf{BLKSTR}\left(2,1\right)+{\displaystyle \sum _{k=2}^{\mathbf{NBLOKS}}}\left[\mathbf{BLKSTR}\left(2,k\right)-\mathbf{BLKSTR}\left(3,k-1\right)\right]=nk$,

(both the number of rows and the number of columns of $A$ must equal $n$).

4:     A(LENA) – REAL (KIND=nag_wp) arrayInput/Output

On entry: the elements of the almost block diagonal matrix stored block by block, with each block stored column by column. The sizes of the blocks and the overlaps are defined by the parameter BLKSTR.

If $a_{rs}$ is the first element in the $k$th block, then an arbitrary element $a_{ij}$ in the $k$th block must be stored in the array element:

$$\mathbf{A}\left(p_k+\left(j-r\right)m_k+\left(i-s\right)+1\right)$$

where

$$p_k=\sum _{l=1}^{k-1}\mathbf{BLKSTR}\left(1,l\right)\times \mathbf{BLKSTR}\left(2,l\right)$$

is the base address of the $k$th block, and

$$m_k=\mathbf{BLKSTR}\left(1,k\right)$$

is the number of rows of the $k$th block.

See Section 8 for comments on scaling.

On exit: the factorized form of the matrix.

5:     LENA – INTEGERInput

On entry: the dimension of the array A as declared in the (sub)program from which F01LHF is called.

Constraint: $\mathbf{LENA}\ge {\displaystyle \sum _{k=1}^{\mathbf{NBLOKS}}}\left[\mathbf{BLKSTR}\left(1,k\right)\times \mathbf{BLKSTR}\left(2,k\right)\right]$.

6:     PIVOT(N) – INTEGER arrayOutput

On exit: details of the interchanges.

7:     TOL – REAL (KIND=nag_wp)Input/Output

On entry: a relative tolerance to be used to indicate whether or not the matrix is singular. For a discussion on how TOL is used see Section 8. If TOL is non-positive, then TOL is reset to $10\epsilon$, where $\epsilon$ is the machine precision.

On exit: unchanged unless $\mathbf{TOL}\le 0.0$ on entry, in which case it is set to $10\epsilon$.

8:     KPIVOT – INTEGEROutput

On exit: if $\mathbf{IFAIL}=\mathbf{2}$, KPIVOT contains the value $k$, where $k$ is the first position on the diagonal of the matrix $A$ where too small a pivot was detected. Otherwise KPIVOT is set to $0$.

9:     IFAIL – INTEGERInput/Output

On entry: IFAIL must be set to $0$, $-1\text{ or }1$. If you are unfamiliar with this parameter you should refer to Section 3.3 in the Essential Introduction for details.

For environments where it might be inappropriate to halt program execution when an error is detected, the value $-1\text{ or }1$ is recommended. If the output of error messages is undesirable, then the value $1$ is recommended. Otherwise, if you are not familiar with this parameter, the recommended value is $0$. When the value $-\mathbf{1}\text{ or }\mathbf{1}$ is used it is essential to test the value of IFAIL on exit.

On exit: $\mathbf{IFAIL}=\mathbf{0}$ unless the routine detects an error or a warning has been flagged (see Section 6).

6  Error Indicators and Warnings

$\mathbf{IFAIL}=1$

On entry,	$\mathbf{N}<1$,
or	$\mathbf{NBLOKS}<1$,
or	$\mathbf{N}<\mathbf{NBLOKS}$,
or	LENA is too small,
or	illegal values detected in BLKSTR.

$\mathbf{IFAIL}=2$

The factorization has been completed, but a small pivot has been detected.

7  Accuracy

8  Further Comments

9  Example

9.1  Program Text

Program Text (f01lhfe.f90)

9.2  Program Data

Program Data (f01lhfe.d)

9.3  Program Results

Program Results (f01lhfe.r)