NAG C Library Function Document

nag_bessel_k1_vector (s18arc)

Keyword Search:

NAG C Library Manual, Mark 26

NAG Library Manual, Mark 26

NAG AD Library Manual, Mark 26

s Chapter Contents

s Chapter Introduction

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

▸▿ 10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1

Purpose

nag_bessel_k1_vector (s18arc) returns an array of values of the modified Bessel function

K_{1} (x)

2

Specification

#include <nag.h>

#include <nags.h>

void	nag_bessel_k1_vector (Integer n, const double x[], double f[], Integer ivalid[], NagError *fail)

3

Description

nag_bessel_k1_vector (s18arc) evaluates an approximation to the modified Bessel function of the second kind

K_{1} (x_{i})

for an array of arguments

x_{i}

, for

i = 1, 2, \dots, n

Note:

K_{1} (x)

is undefined for

x \leq 0

and the function will fail for such arguments.

The function is based on five Chebyshev expansions:

For

0 < x \leq 1

K_{1} (x) = \frac{1}{x} + x \ln x \underset{r = 0}{\sum^{'}} a_{r} T_{r} (t) - x \underset{r = 0}{\sum^{'}} b_{r} T_{r} (t),   where ​ t = 2 x^{2} - 1 .

For

1 < x \leq 2

K_{1} (x) = e^{- x} \underset{r = 0}{\sum^{'}} c_{r} T_{r} (t),   where ​ t = 2 x - 3 .

For

2 < x \leq 4

K_{1} (x) = e^{- x} \underset{r = 0}{\sum^{'}} d_{r} T_{r} (t),   where ​ t = x - 3 .

For

x > 4

K_{1} (x) = \frac{e^{- x}}{\sqrt{x}} \underset{r = 0}{\sum^{'}} e_{r} T_{r} (t),   where ​ t = \frac{9 - x}{1 + x} .

For

x

near zero,

K_{1} (x) ≃ \frac{1}{x}

. This approximation is used when

x

is sufficiently small for the result to be correct to machine precision. For very small

x

it is impossible to calculate

\frac{1}{x}

without overflow and the function must fail.

For large

x

, where there is a danger of underflow due to the smallness of

K_{1}

, the result is set exactly to zero.

4

References

NIST Digital Library of Mathematical Functions

5

Arguments

1: $n$ – IntegerInput

On entry:

n

, the number of points.

Constraint:

n \geq 0

2: $x [n]$ – const doubleInput

On entry: the argument

x_{i}

of the function, for

i = 1, 2, \dots, n

Constraint:

x [i - 1] > 0.0

, for

i = 1, 2, \dots, n

3: $f [n]$ – doubleOutput

On exit:

K_{1} (x_{i})

, the function values.

4: $ivalid [n]$ – IntegerOutput

On exit:

ivalid [i - 1]

contains the error code for

x_{i}

, for

i = 1, 2, \dots, n

$ivalid [i - 1] = 0$: No error.
$ivalid [i - 1] = 1$: $x_{i} \leq 0.0$ , $K_{1} (x_{i})$ is undefined. $f [i - 1]$ contains $0.0$ .
$ivalid [i - 1] = 2$: $x_{i}$ is too small, there is a danger of overflow. $f [i - 1]$ contains zero. The threshold value is the same as for $fail . code =$ NE_REAL_ARG_TOO_SMALL in nag_bessel_k1 (s18adc), as defined in the Users' Note for your implementation.

5: $fail$ – NagError *Input/Output

The NAG error argument (see Section 3.7 in How to Use the NAG Library and its Documentation).

6

Error Indicators and Warnings

NE_ALLOC_FAIL: Dynamic memory allocation failed.
See Section 2.3.1.2 in How to Use the NAG Library and its Documentation for further information.
NE_BAD_PARAM: On entry, argument $〈value〉$ had an illegal value.
NE_INT: On entry, $n = 〈value〉$ .
Constraint: $n \geq 0$ .
NE_INTERNAL_ERROR: An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact NAG for assistance.
See Section 2.7.6 in How to Use the NAG Library and its Documentation for further information.
NE_NO_LICENCE: Your licence key may have expired or may not have been installed correctly.
See Section 2.7.5 in How to Use the NAG Library and its Documentation for further information.
NW_IVALID: On entry, at least one value of x was invalid.
Check ivalid for more information.

7

Accuracy

Let

δ

and

ε

be the relative errors in the argument and result respectively.

δ

is somewhat larger than the machine precision (i.e., if

δ

is due to data errors etc.), then

ε

and

δ

are approximately related by:

ε ≃ |\frac{x K_{0} (x) - K_{1} (x)}{K_{1} (x)}| δ .

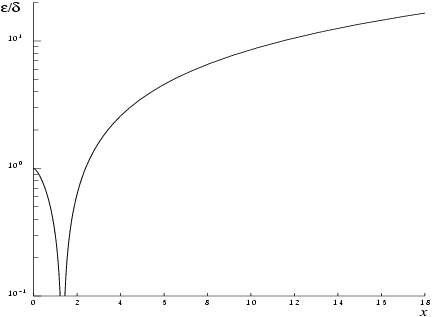
Figure 1 shows the behaviour of the error amplification factor

|\frac{x K_{0} (x) - K_{1} (x)}{K_{1} (x)}| .

However, if

δ

is of the same order as the machine precision, then rounding errors could make

ε

slightly larger than the above relation predicts.

For small

x

ε ≃ δ

and there is no amplification of errors.

For large

x

ε ≃ x δ

and we have strong amplification of the relative error. Eventually

K_{1}

, which is asymptotically given by

\frac{e^{- x}}{\sqrt{x}}

, becomes so small that it cannot be calculated without underflow and hence the function will return zero. Note that for large

x

the errors will be dominated by those of the standard function exp.

Figure 1

8

Parallelism and Performance

nag_bessel_k1_vector (s18arc) is not threaded in any implementation.

9

Further Comments

None.

10

Example

This example reads values of x from a file, evaluates the function at each value of

x_{i}

and prints the results.

NAG C Library Function Document

nag_bessel_k1_vector (s18arc)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1

Purpose

2

Specification

3

Description

4

References

5

Arguments

6

Error Indicators and Warnings

7

Accuracy

8

Parallelism and Performance

9

Further Comments

10

Example

10.1

Program Text

10.2

Program Data

10.3

Program Results