NAG Library ManualKeyword Search:

NAG Library Function Document

nag_bessel_j1_vector (s17atc)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

▸▿ 10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1 Purpose

nag_bessel_j1_vector (s17atc) returns an array of values of the Bessel function

J_{1} (x)

2 Specification

#include <nag.h>

#include <nags.h>

void	nag_bessel_j1_vector (Integer n, const double x[], double f[], Integer ivalid[], NagError *fail)

3 Description

nag_bessel_j1_vector (s17atc) evaluates an approximation to the Bessel function of the first kind

J_{1} (x_{i})

for an array of arguments

x_{i}

, for

i = 1, 2, \dots, n

Note:

J_{1} (- x) = - J_{1} (x)

, so the approximation need only consider

x \geq 0

The function is based on three Chebyshev expansions:

For

0 < x \leq 8

J_{1} (x) = \frac{x}{8} \underset{r = 0}{\sum^{'}} a_{r} T_{r} (t),   with ​ t = 2 {(\frac{x}{8})}^{2} - 1 .

For

x > 8

J_{1} (x) = \sqrt{\frac{2}{π x}} \{P_{1} (x) \cos (x - \frac{3 π}{4}) - Q_{1} (x) \sin (x - \frac{3 π}{4})\}

where

P_{1} (x) = \underset{r = 0}{\sum^{'}} b_{r} T_{r} (t)

and

Q_{1} (x) = \frac{8}{x} \underset{r = 0}{\sum^{'}} c_{r} T_{r} (t)

with

t = 2 {(\frac{8}{x})}^{2} - 1

For

x

near zero,

J_{1} (x) ≃ \frac{x}{2}

. This approximation is used when

x

is sufficiently small for the result to be correct to machine precision.

For very large

x

, it becomes impossible to provide results with any reasonable accuracy (see Section 7), hence the function fails. Such arguments contain insufficient information to determine the phase of oscillation of

J_{1} (x)

; only the amplitude,

\sqrt{\frac{2}{π |x|}}

, can be determined and this is returned on failure. The range for which this occurs is roughly related to machine precision; the function will fail if

|x| ≳ 1 / machine precision

(see the Users' Note for your implementation for details).

4 References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

Clenshaw C W (1962) Chebyshev Series for Mathematical Functions Mathematical tables HMSO

5 Arguments

1: $n$ – IntegerInput

On entry:

n

, the number of points.

Constraint:

n \geq 0

2: $x [n]$ – const doubleInput

On entry: the argument

x_{i}

of the function, for

i = 1, 2, \dots, n

3: $f [n]$ – doubleOutput

On exit:

J_{1} (x_{i})

, the function values.

4: $ivalid [n]$ – IntegerOutput

On exit:

ivalid [i - 1]

contains the error code for

x_{i}

, for

i = 1, 2, \dots, n

$ivalid [i - 1] = 0$

No error.

$ivalid [i - 1] = 1$

On entry,

x_{i}

is too large.

f [i - 1]

contains the amplitude of the

J_{1}

oscillation,

\sqrt{\frac{2}{π |x_{i}|}}

5: $fail$ – NagError *Input/Output

The NAG error argument (see Section 2.7 in How to Use the NAG Library and its Documentation).

6 Error Indicators and Warnings

NE_ALLOC_FAIL: Dynamic memory allocation failed.
See Section 2.3.1.2 in How to Use the NAG Library and its Documentation for further information.
NE_BAD_PARAM: On entry, argument $〈value〉$ had an illegal value.
NE_INT: On entry, $n = 〈value〉$ .
Constraint: $n \geq 0$ .
NE_INTERNAL_ERROR: An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact NAG for assistance.

An unexpected error has been triggered by this function. Please contact NAG.
See Section 2.7.6 in How to Use the NAG Library and its Documentation for further information.
NE_NO_LICENCE: Your licence key may have expired or may not have been installed correctly.
See Section 2.7.5 in How to Use the NAG Library and its Documentation for further information.
NW_IVALID: On entry, at least one value of x was invalid.
Check ivalid for more information.

7 Accuracy

Let

δ

be the relative error in the argument and

E

be the absolute error in the result. (Since

J_{1} (x)

oscillates about zero, absolute error and not relative error is significant.)

δ

is somewhat larger than machine precision (e.g., if

δ

is due to data errors etc.), then

E

and

δ

are approximately related by:

E ≃ |x J_{0} (x) - J_{1} (x)| δ

(provided

E

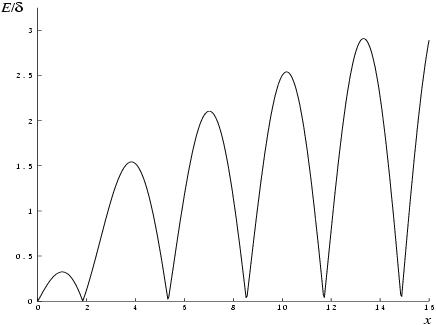
is also within machine bounds). Figure 1 displays the behaviour of the amplification factor

|x J_{0} (x) - J_{1} (x)|

However, if

δ

is of the same order as machine precision, then rounding errors could make

E

slightly larger than the above relation predicts.

For very large

x

, the above relation ceases to apply. In this region,

J_{1} (x) ≃ \sqrt{\frac{2}{π |x|}} \cos (x - \frac{3 π}{4})

. The amplitude

\sqrt{\frac{2}{π |x|}}

can be calculated with reasonable accuracy for all

x

, but

\cos (x - \frac{3 π}{4})

cannot. If

x - \frac{3 π}{4}

is written as

2 N π + θ

where

N

is an integer and

0 \leq θ < 2 π

, then

\cos (x - \frac{3 π}{4})

is determined by

θ

only. If

x ≳ δ^{- 1}

θ

cannot be determined with any accuracy at all. Thus if

x

is greater than, or of the order of, the reciprocal of machine precision, it is impossible to calculate the phase of

J_{1} (x)

and the function must fail.

Figure 1

8 Parallelism and Performance

nag_bessel_j1_vector (s17atc) is not threaded in any implementation.

9 Further Comments

None.

10 Example

This example reads values of x from a file, evaluates the function at each value of

x_{i}

and prints the results.

NAG Library Function Documentnag_bessel_j1_vector (s17atc)