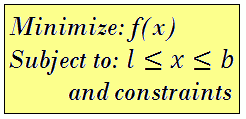
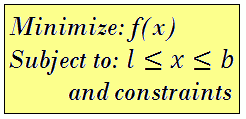 |
A nonlinear minimization problem solving routine - nag_opt_nlp (e04ucc). |
We demonstrate two ways of supplying the pair of functions - either as C code or as Octave code. There are advantages to both of these approaches. Since we need to write C code anyway, in order to interface between Octave and NAG, adding the user-supplied functions as C code is relatively easy. This approach avoids some of the problems associated with converting between C types and Octave types.
The disadvantage of writing the user-supplied functions as C code is that you need to rewrite the functions and regenerate the interface code every time you want to solve a different minimization problem. Although it is harder at first, a more flexible approach is to write an interface that lets the user-supplied functions be written as Octave code.
#include <nag.h>
#include <nage04.h>
void nag_opt_nlp(Integer n, Integer nclin, Integer ncnlin, const double a[], Integer tda, const double bl[], const double bu[],
void(*objfun)(Integer n, const double x[], double *objf, double g[], Nag_Comm *comm),
void(*confun)(Integer n, Integer ncnlin, const Integer needc[], const double x[], double conf[], double conjac[], Nag_Comm *comm),
double x[], double *objf, double g[], Nag_E04_Opt *options, Nag_Comm *comm, NagError *fail);
For argument descriptions consult the e04ucc document in the
NAG C Library Manual [6].
To keep things simple, we are going to return only the integer value of fail.code.
#include <octave/oct.h>
#define Complex NagComplex
#define MatrixType NagMatrixType
#include <nag.h>
#include <nage04.h>
extern "C" {
static void objfun(Integer n, double x[], double *objf,
double objgrd[], Nag_Comm *comm);
static void confun(Integer n, Integer ncnlin, Integer needc[],
double x[], double conf[], double conjac[],
Nag_Comm *comm);
}
DEFUN_DLD (nag_opt, args, ,
"Calls nag_opt_nlp (e04ucc), which minimizes an arbitrary smooth function \n\
subject to constraints using a sequential quadratic programming (SQP) method.\n\
As many first derivatives as possible should be supplied by you; \n\
any unspecified derivatives are approximated by finite differences. \n\
It is not intended for large sparse problems.\n\
nag_opt_nlp (e04ucc) may also be used for unconstrained, bound-constrained \n\
and linearly constrained optimization.\n")
{
// Variable to store function output values
octave_value_list retval;
// Retrieve input arguments from args
Integer n = args(0).int_value();
Integer nclin = args(1).int_value();
Integer ncnlin = args(2).int_value();
Matrix a(args(3).matrix_value());
Integer tda = args(4).int_value();
NDArray bl(args(5).array_value());
NDArray bu(args(6).array_value());
NDArray x(args(7).array_value());
dim_vector dv (1); dv(0) = n;
NDArray objgrd(dv);
// Declare local variables
double objf;
Nag_Comm comm;
NagError fail;
INIT_FAIL(fail);
// Call NAG routine
nag_opt_nlp(n, nclin, ncnlin, a.fortran_vec(), tda, bl.fortran_vec(),
bu.fortran_vec(), objfun, confun, x.fortran_vec(), &objf,
objgrd.fortran_vec(), E04_DEFAULT, &comm, &fail);
// Assign output arguments to retval
retval(0) = objf;
retval(1) = objgrd;
retval(2) = fail.code;
return retval;
}
static void objfun(Integer n, double x[], double *objf,
double objgrd[], Nag_Comm *comm)
{
/* Routine to evaluate objective function and its 1st derivatives. */
if (comm->flag == 0 || comm->flag == 2)
*objf = x[0] * x[3] * (x[0] + x[1] + x[2]) + x[2];
if (comm->flag == 2)
{
objgrd[0] = x[3] * (2.0*x[0] + x[1] + x[2]);
objgrd[1] = x[0] * x[3];
objgrd[2] = x[0] * x[3] + 1.0;
objgrd[3] = x[0] * (x[0] + x[1] + x[2]);
}
} /* objfun */
static void confun(Integer n, Integer ncnlin, Integer needc[],
double x[], double conf[], double conjac[],
Nag_Comm *comm)
{
/* Routine to evaluate the nonlinear constraints and
* their 1st derivatives.
*/
#define CONJAC(I,J) conjac[(I-1)*n + J - 1]
Integer i, j;
if (comm->first)
{
/* First call to confun. Set all Jacobian elements to zero.
* Note that this will only work when con_deriv = TRUE
* (the default; see Section 4 (confun) and 8.2 (con_deriv)).
*/
for (j = 1; j <= n; ++j)
for (i = 1; i <= ncnlin; ++i)
CONJAC(i,j) = 0.0;
}
if (needc[0] > 0)
{
if (comm->flag == 0 || comm->flag == 2)
conf[0] = x[0] * x[0] + x[1] * x[1] + x[2] * x[2] + x[3] * x[3];
if (comm->flag == 2)
{
CONJAC(1,1) = x[0] * 2.0;
CONJAC(1,2) = x[1] * 2.0;
CONJAC(1,3) = x[2] * 2.0;
CONJAC(1,4) = x[3] * 2.0;
}
}
if (needc[1] > 0)
{
if (comm->flag == 0 || comm->flag == 2)
conf[1] = x[0] * x[1] * x[2] * x[3];
if (comm->flag == 2)
{
CONJAC(2,1) = x[1] * x[2] * x[3];
CONJAC(2,2) = x[0] * x[2] * x[3];
CONJAC(2,3) = x[0] * x[1] * x[3];
CONJAC(2,4) = x[0] * x[1] * x[2];
}
}
} /* confun */
Points to note about this code:
% mkoctfile nag_opt.cc -L/opt/NAG/cll6a08dg/lib -lnagc_nag -I/opt/NAG/cll6a08dg/includewhere:
octave:1> a = [1.0;1.0;1.0;1.0]; octave:2> bl = [1.0,1.0,1.0,1.0,-1.0E+25,-1.0E+25,25.0]; octave:3> bu = [5.0,5.0,5.0,5.0,20.0,40.0,1.0E+25]; octave:4> x = [1.0,5.0,5.0,1.0]; octave:5> [objf,objgrd,ifail] = nag_opt(4,1,2,a,4,bl,bu,x)
(If you get an error message saying that a library cannot be located, see the tip given in Example 1).
#include <octave/oct.h>
#include <octave/parse.h>
#define Complex NagComplex
#define MatrixType NagMatrixType
#include <nag.h>
#include <nage04.h>
extern "C" {
static void objfunC(Integer n, double x[], double *objf,
double objgrd[], Nag_Comm *comm);
static void confunC(Integer n, Integer ncnlin, Integer needc[],
double x[], double conf[], double conjac[],
Nag_Comm *comm);
}
DEFUN_DLD (nag_opt2, args, ,
"Calls nag_opt_nlp (e04ucc), which minimizes an arbitrary smooth function \n\
subject to constraints using a sequential quadratic programming (SQP) method.\n \
As many first derivatives as possible should be supplied by you; \n \
any unspecified derivatives are approximated by finite differences. \n \
It is not intended for large sparse problems.\n \
nag_opt_nlp (e04ucc) may also be used for unconstrained, bound-constrained \n \
and linearly constrained optimization.\n")
{
// Variable to store function output values
octave_value_list retval;
// Retrieve input arguments from args
Integer n = args(0).int_value();
Integer nclin = args(1).int_value();
Integer ncnlin = args(2).int_value();
Matrix a(args(3).matrix_value());
Integer tda = args(4).int_value();
NDArray bl(args(5).array_value());
NDArray bu(args(6).array_value());
struct fcnptrs {octave_function *obj, *con;} fcns;
fcns.obj = args(7).function_value();
fcns.con = args(8).function_value();
NDArray x(args(9).array_value());
dim_vector dv (1); dv(0) = n;
NDArray objgrd(dv);
// Declare local variables
double objf=0.0;
Nag_Comm comm;
NagError fail;
INIT_FAIL(fail);
// Store Octave functions handles in communication structure comm
comm.p = (Pointer) &fcns;
// Call NAG routine
nag_opt_nlp(n, nclin, ncnlin, a.fortran_vec(), tda, bl.fortran_vec(),
bu.fortran_vec(),objfunC, confunC, x.fortran_vec(),&objf,
objgrd.fortran_vec(), E04_DEFAULT, &comm, &fail);
// Assign output arguments to retval
retval(0) = objf;
retval(1) = objgrd;
retval(2) = fail.code;
return retval;
}
static void objfunC(Integer n, double x[], double *objf,
double objgrd[], Nag_Comm *comm)
{
// Retrieve Octave objfun handle
struct fcnptrs {octave_function *obj, *con;} *fcns;
fcns = (struct fcnptrs *) comm->p;
octave_function *fcn = (octave_function *) fcns->obj;
// Copy C arrays into the Octave type ones
dim_vector dv (1); dv(0) = n;
NDArray x_oct(dv), objgrd_oct(dv);
octave_idx_type i;
for (i=0;i<n;i++) {
x_oct.elem(i) = x[i];
objgrd_oct.elem(i) = objgrd[i];
}
// Assign objfun input arguments
octave_value_list newargs, retval;
newargs(0)=octave_value(comm->flag);
newargs(1)=octave_value(x_oct);
newargs(2)=octave_value(*objf);
newargs(3)=octave_value(objgrd_oct);
int nargout=2;
// Call Octave objfun function
retval=feval(fcn,newargs,nargout);
// Retrieve output arguments from retval
*objf=retval(0).double_value();
objgrd_oct = retval(1).array_value();
// Copy output arrays back into C type arrays
for (i=0;i<n;i++) {
objgrd[i]=objgrd_oct.elem(i);
x[i]=x_oct.elem(i);
}
} /* objfunC */
static void confunC(Integer n, Integer ncnlin, Integer needc[],
double x[], double conf[], double conjac[],
Nag_Comm *comm)
{
#define CONJAC(I,J) conjac[(I-1)*n + J - 1]
// Retrieve Octave confun handle
struct fcnptrs {octave_function *obj, *con;} *fcns;
fcns = (struct fcnptrs *) comm->p;
octave_function *fcn = (octave_function *) fcns->con;
// Copy C arrays into the Octave type arrays and matrices
dim_vector dv (1); dv(0) = ncnlin;
dim_vector dv2 (1); dv2(0) = n;
NDArray needc_oct(dv), conf_oct(dv), x_oct(dv2);
Matrix conjac_oct(ncnlin,n);
octave_idx_type i,j;
for (i=0;i<ncnlin;i++) {
needc_oct.elem(i) = needc[i];
conf_oct.elem(i) = conf[i];
for (j=0;j<n;j++) {
x_oct.elem(j) = x[j];
conjac_oct.elem(i,j) = CONJAC(i+1,j+1);
}
}
// Assign confun input arguments
octave_value_list newargs, retval;
newargs(0)=octave_value(comm->flag);
newargs(1)=octave_value(ncnlin);
newargs(2)=octave_value(n);
newargs(3)=octave_value(needc_oct);
newargs(4)=octave_value(x_oct);
newargs(5)=octave_value(conjac_oct);
newargs(6)=octave_value(comm->first);
int nargout=2;
// Call Octave confun function
retval=feval(fcn,newargs,nargout);
// Retrieve output arguments from retval
conf_oct=retval(0).array_value();
conjac_oct = retval(1).matrix_value();
// Copy output arrays and matrices back into C type arrays
for (i=0;i<ncnlin;i++) {
needc[i] = needc_oct.elem(i);
conf[i] = conf_oct.elem(i);
for (j=0;j<n;j++) {
x[j]=x_oct.elem(j);
CONJAC(i+1,j+1) = conjac_oct.elem(i,j);
}
}
} /* confunC */
Points to note about this code (other than in the previous code):
function [objf,objgrd]=objfun(mode,x,objf,objgrd)
% Routine to evaluate objective function and its 1st derivatives.
if mode == 0 || mode == 2
objf = x(1) * x(4) * (x(1) + x(2) + x(3)) + x(3);
end
if mode == 2
objgrd(1) = x(4) * (2.0*x(1) + x(2) + x(3));
objgrd(2) = x(1) * x(4);
objgrd(3) = x(1) * x(4) + 1.0;
objgrd(4) = x(1) * (x(1) + x(2) + x(3));
end
endfunction
function [c, cjac] = confun(mode, ncnln, n, needc, x, cjac, nstate)
% Routine to evaluate the nonlinear constraints and their 1st derivatives.
% Function Body
if nstate
% First call to confun. Set all Jacobian elements to zero.
cjac = zeros(ncnln,n);
end
if needc(1) > 0
if mode == 0 || mode == 2
c(1) = x(1) * x(1) + x(2) * x(2) + x(3) * x(3) + x(4) * x(4);
end
if mode == 2
cjac(1,1) = x(1) * 2.0;
cjac(1,2) = x(2) * 2.0;
cjac(1,3) = x(3) * 2.0;
cjac(1,4) = x(4) * 2.0;
end
end
if needc(2) > 0
if mode == 0 || mode == 2
c(2) = x(1) * x(2) * x(3) * x(4);
end
if mode == 2
cjac(2,1) = x(2) * x(3) * x(4);
cjac(2,2) = x(1) * x(3) * x(4);
cjac(2,3) = x(1) * x(2) * x(4);
cjac(2,4) = x(1) * x(2) * x(3);
end
end
endfunction
% mkoctfile nag_opt2.cc -L/opt/NAG/cll6a08dg/lib -lnagc_nag -I/opt/NAG/cll6a08dg/includewhere:
octave:1> a = [1.0;1.0;1.0;1.0]; octave:2> bl = [1.0,1.0,1.0,1.0,-1.0E+25,-1.0E+25,25.0]; octave:3> bu = [5.0,5.0,5.0,5.0,20.0,40.0,1.0E+25]; octave:4> x = [1.0,5.0,5.0,1.0]; octave:5> [objf,objgrd,ifail] = nag_opt2(4,1,2,a,4,bl,bu,@objfun,@confun,x)
Parameters to e04ucc
--------------------
Number of variables........... 4
Linear constraints............ 1 Nonlinear constraints......... 2
start................... Nag_Cold
step_limit.............. 2.00e+00 machine precision....... 1.11e-16
lin_feas_tol............ 1.05e-08 nonlin_feas_tol......... 1.05e-08
optim_tol............... 3.26e-12 linesearch_tol.......... 9.00e-01
crash_tol............... 1.00e-02 f_prec.................. 4.37e-15
inf_bound............... 1.00e+20 inf_step................ 1.00e+20
max_iter................ 50 minor_max_iter.......... 50
hessian................. Nag_FALSE
f_diff_int.............. Automatic c_diff_int.............. Automatic
obj_deriv............... Nag_TRUE con_deriv............... Nag_TRUE
verify_grad....... Nag_SimpleCheck print_deriv............ Nag_D_Full
print_level......... Nag_Soln_Iter minor_print_level..... Nag_NoPrint
outfile................. stdout
Verification of the objective gradients.
----------------------------------------
All objective gradient elements have been set.
Simple Check:
The objective gradient seems to be ok.
Directional derivative of the objective 8.15250000e-01
Difference approximation 8.15249734e-01
Verification of the constraint gradients.
-----------------------------------------
All constraint gradient elements have been set.
Simple Check:
The Jacobian seems to be ok.
The largest relative error was 2.29e-07 in constraint 2
Maj Mnr Step Merit function Violtn Norm Gz Cond Hz
0 4 0.0e+00 1.738281e+01 1.2e+01 7.1e-01 1.0e+00
1 1 1.0e+00 1.703169e+01 1.9e+00 4.6e-02 1.0e+00
2 1 1.0e+00 1.701442e+01 8.8e-02 2.1e-02 1.0e+00
3 1 1.0e+00 1.701402e+01 5.4e-04 3.1e-04 1.0e+00
4 1 1.0e+00 1.701402e+01 9.9e-08 7.0e-06 1.0e+00
5 1 1.0e+00 1.701402e+01 4.6e-11 1.1e-08 1.0e+00
Exit from NP problem after 5 major iterations, 9 minor iterations.
Varbl State Value Lower Bound Upper Bound Lagr Mult Residual
V 1 LL 1.00000e+00 1.00000e+00 5.00000e+00 1.0879e+00 0.0000e+00
V 2 FR 4.74300e+00 1.00000e+00 5.00000e+00 0.0000e+00 2.5700e-01
V 3 FR 3.82115e+00 1.00000e+00 5.00000e+00 0.0000e+00 1.1789e+00
V 4 FR 1.37941e+00 1.00000e+00 5.00000e+00 0.0000e+00 3.7941e-01
L Con State Value Lower Bound Upper Bound Lagr Mult Residual
L 1 FR 1.09436e+01 None 2.00000e+01 0.0000e+00 9.0564e+00
N Con State Value Lower Bound Upper Bound Lagr Mult Residual
N 1 UL 4.00000e+01 None 4.00000e+01 -1.6147e-01 -3.5264e-11
N 2 LL 2.50000e+01 2.50000e+01 None 5.5229e-01 -2.8791e-11
Optimal solution found.
Final objective value = 1.7014017e+01
objf = 17.014
objgrd =
14.5723
1.3794
2.3794
9.5641
ifail = 0